Cho tam giác ABC nhọn có hai đường cao BE, CF cắt nhau tại H. Chứng minh rằng a) ΔAEB ᔕ ΔAFC.
Cho tam giác ABC nhọn có hai đường cao BE, CF cắt nhau tại H. Chứng minh rằng
a) ΔAEB ᔕ ΔAFC.
b) HEHC=HFHB.
c) ΔHEF ᔕ ΔHCB.
Cho tam giác ABC nhọn có hai đường cao BE, CF cắt nhau tại H. Chứng minh rằng
a) ΔAEB ᔕ ΔAFC.
b) HEHC=HFHB.
c) ΔHEF ᔕ ΔHCB.
Lời giải:
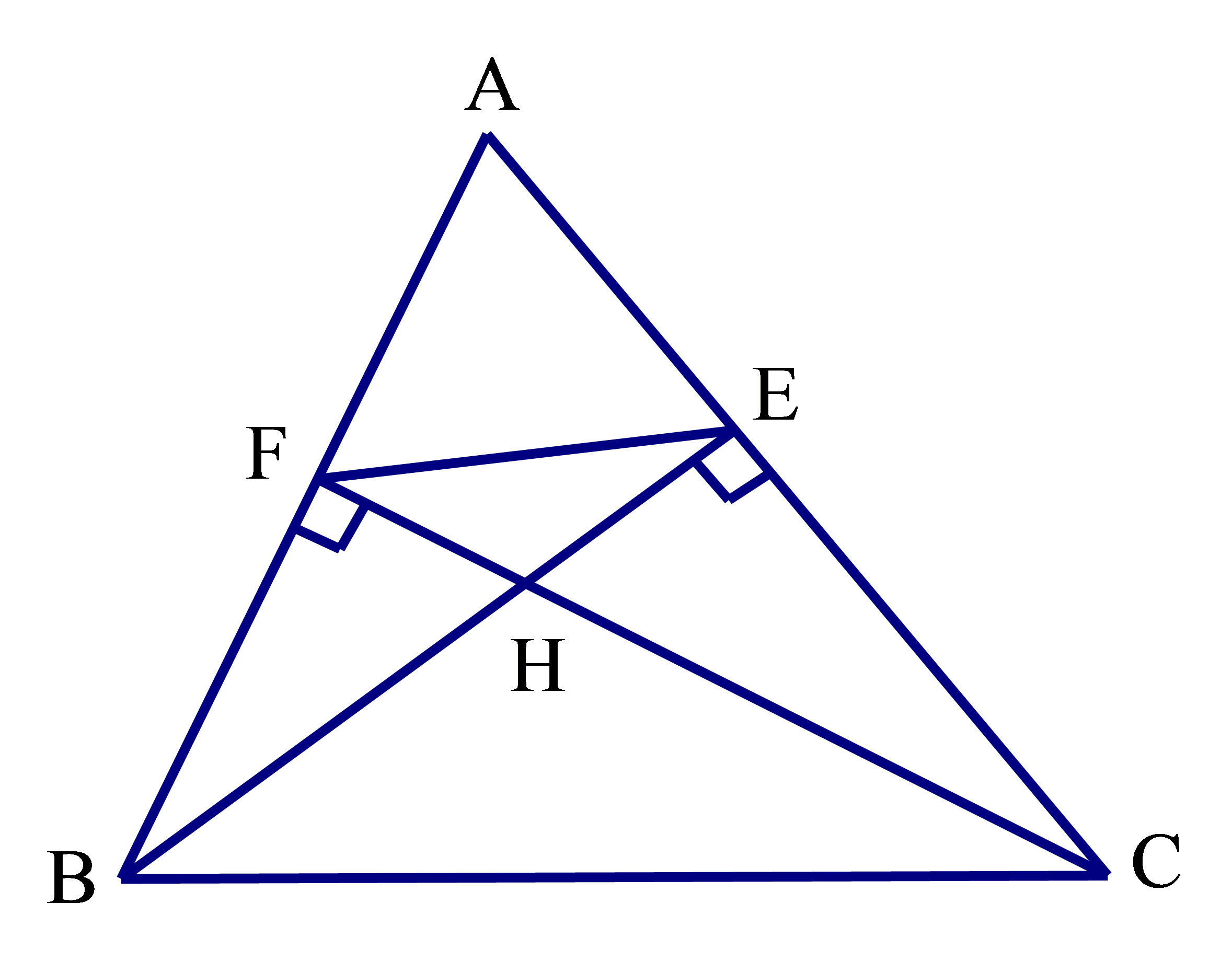
a) Xét tam giác vuông AEB và AFC có:
ˆA chung
Suy ra ΔAEB ᔕ ΔAFC (g.g)
b) Xét tam giác vuông HCE và HBF ta có:
^EHC=^FHB (hai góc đối đỉnh)
Suy ra ΔHCE ᔕ ΔHBF (g.g)
Nên HEHF=HCHB hay HEHC=HFHB
c) Xét tam giác HEF và HCB ta có:
HEHC=HFHB (cmt)
^EHF=^BHC (hai góc đối đỉnh)
Suy ra ΔHEF ᔕ ΔHCB (c.g.c).