Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H. a) Chứng minh rằng ΔAMN ᔕ ΔABC.
24
31/10/2024
Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H.
a) Chứng minh rằng ΔAMN ᔕ ΔABC.
b) Phân giác của ^BAC cắt MN và BC lần lượt tại I và K. Chứng minh rằng IMIN=KBKC.
Trả lời
Lời giải:
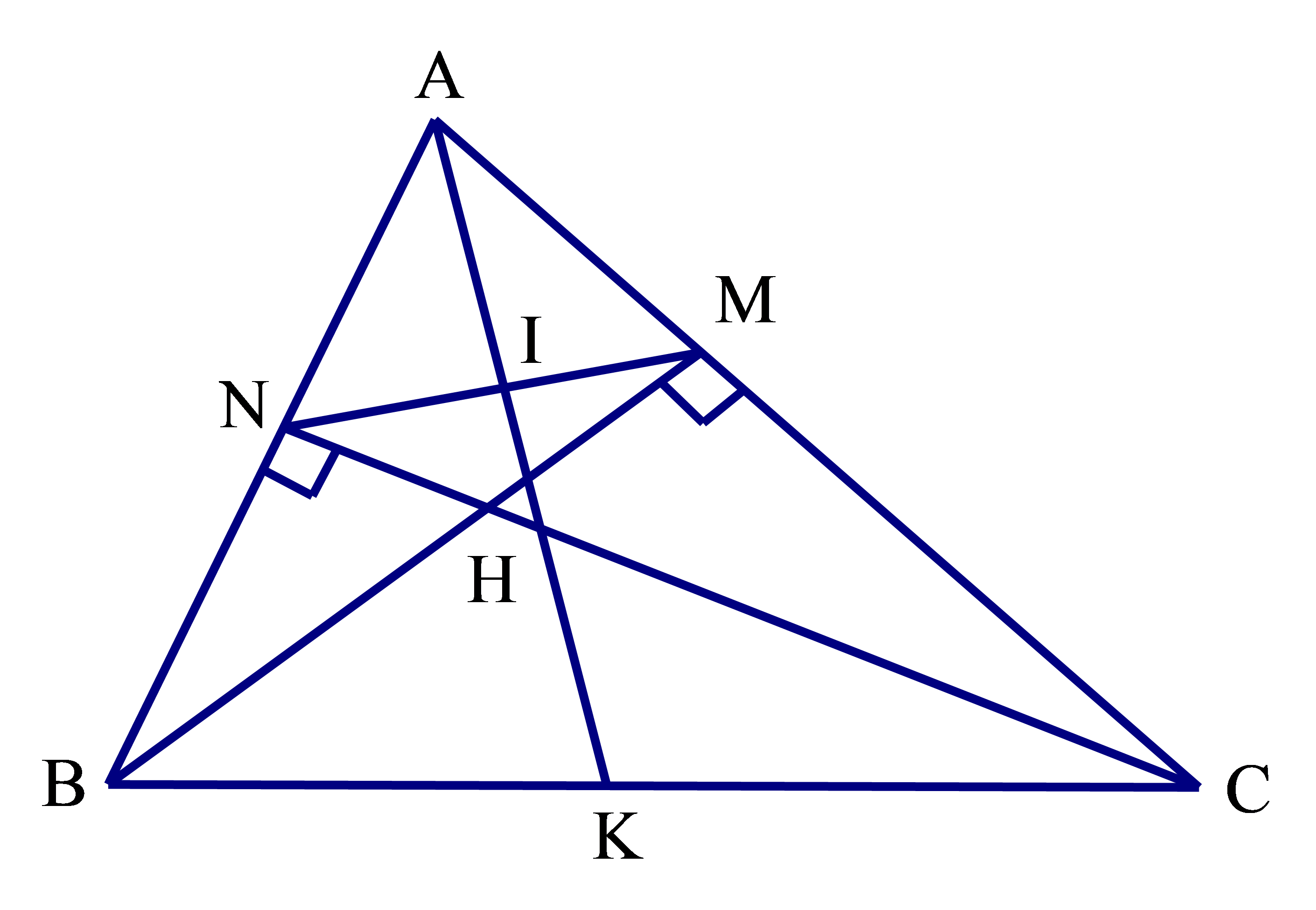
a) Xét tam giác vuông ABM và ACN có:
ˆA chung
Suy ra ΔABM ᔕ ΔACN (g.g)
Nên AMAN=ABAC hay AMAB=ANAC
Xét tam giác AMN và ABC ta có:
AMAB=ANAC
ˆA chung
Suy ra ΔAMN ᔕ ΔABC (c.g.c).
b) ΔAMN ᔕ ΔABC, AK là phân giác của ^BAC
Suy ra AMAB=ANAC=AIAK
Xét tam giác AIM và AKB ta có:
AMAB=AIAK
^IAM=^IAN (vì AK là phân giác ^BAC)
Suy ra ΔAIM ᔕ ΔAKB nên IMKB=AIAK (1)
Xét tam giác AIN và AKC ta có:
ANAC=AIAK
^IAM=^IAN (vì AK là phân giác ^BAC)
Suy ra ΔAIN ᔕ ΔAKC nên INKC=AIAK (2)
Từ (1) và (2) suy ra IMKB=INKC hay IMIN=KBKC.

