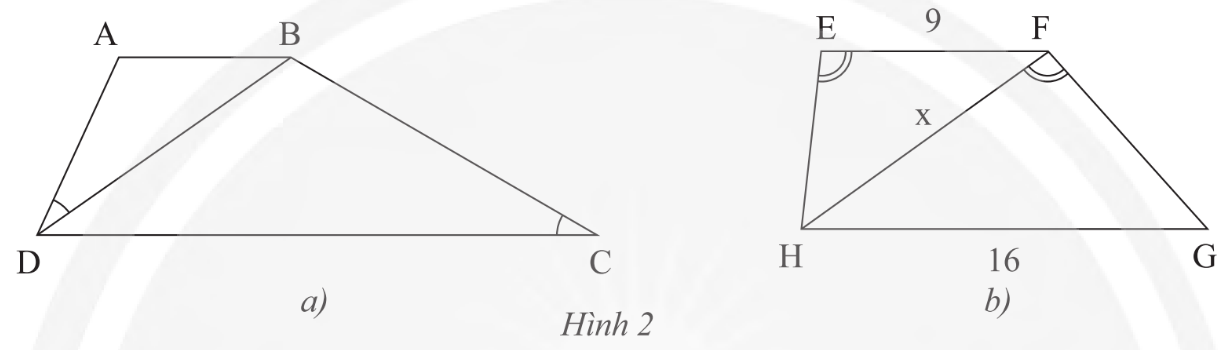
a) Cho hình thang ABCD (AB // CD), biết góc ADB = góc DCB (Hình 2a). Chứng minh rằng BD2 = AB.CD. b) Cho hình thang EFGH (EF // GH)
21
31/10/2024
a) Cho hình thang ABCD (AB // CD), biết ^ADB=^DCB (Hình 2a). Chứng minh rằng BD2 = AB.CD.
b) Cho hình thang EFGH (EF // GH), ^HEF=^HFG, EF = 9 m, GH = 16 m (Hình 2b). Tính độ dài x của HF.
Trả lời
Lời giải:
a) Xét ΔABD và ΔBDC có:
^ADB=^DCB (gt)
^ABD=^BDC (AB // CD, hai góc so le trong)
Do đso ΔABD ᔕ ΔBDC (g.g)
Suy ra ABBD=BDCD (các cạnh tương ứng).
Vậy BD2 = AB.CD (đpcm).
b) Tương tự câu a, ta có: ^EHG=^FGH
Xét tam giác EFH và FHG ta có:
^EHG=^FGH
^HEF=^HFG
Do đó ΔEFH ᔕ ΔFHG (g.g)
Suy ra EFHF=HFGH (các cạnh tương ứng).
Khi đó HF2 = EF.GH = 9.16 = 144 nên HF = 12 cm.

