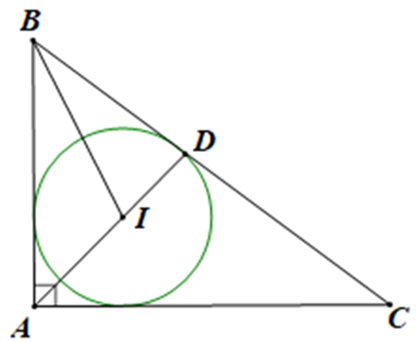
Do tam giác ABC vuông tại A nên BC² = AB² + AC² (Định lí Pythagore).

Suy ra \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{3^2} + {4^2}} = 5\).

Gọi AD là đường phân giác của tam giác ABC.

Áp dụng tính chất đường phân giác, ta được: \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{3}{4}\).

Khi đó \(\overrightarrow {BD} = \frac{3}{4}\overrightarrow {DC} \).

\( \Leftrightarrow \overrightarrow {ID} - \overrightarrow {IB} = \frac{3}{4}\overrightarrow {IC} - \frac{3}{4}\overrightarrow {ID} \).

\( \Leftrightarrow \frac{7}{4}\overrightarrow {ID} = \overrightarrow {IB} + \frac{3}{4}\overrightarrow {IC} \).

\( \Leftrightarrow 7\overrightarrow {ID} = 4\overrightarrow {IB} + 3\overrightarrow {IC} \)         (1)

Lại có BI là đường phân giác của tam giác ABD (do I là tâm đường tròn ngoại tiếp tam giác ABC).

Áp dụng tính chất đường phân giác, ta được: \(\frac{{ID}}{{IA}} = \frac{{BD}}{{BA}} = \frac{{DC}}{{AC}}\).

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\frac{{ID}}{{IA}} = \frac{{BD}}{{BA}} = \frac{{DC}}{{AC}} = \frac{{BD + DC}}{{BA + AC}} = \frac{{BC}}{{BA + AC}} = \frac{5}{7}\).

Khi đó \(7\overrightarrow {ID} = - 5\overrightarrow {IA} \) (2)

Từ (1), (2), suy ra \(4\overrightarrow {IB} + 3\overrightarrow {IC} = - 5\overrightarrow {IA} \).

Vậy \(5\overrightarrow {IA} + 4\overrightarrow {IB} + 3\overrightarrow {IC} = \vec 0\) (điều phải chứng minh).