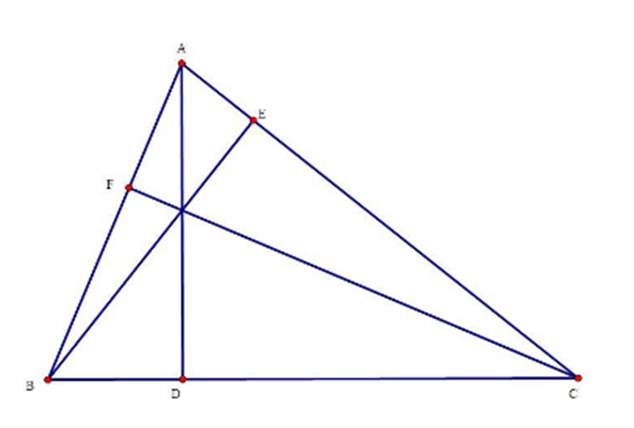
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Chứng minh rằng
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H.
Chứng minh rằng: \(\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}} \ge \sqrt 3 \).
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H.
Chứng minh rằng: \(\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}} \ge \sqrt 3 \).
\[{\left( {\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}}} \right)^2} \ge 3\sqrt {\frac{{HA}}{{BC}}.\frac{{HB}}{{AC}} + \frac{{HB}}{{AC}}.\frac{{HC}}{{AB}} + \frac{{HC}}{{AB}}.\frac{{HA}}{{BC}}} \](*)
Xét tam giác HAE và tam giác CAD có:
Chung \(\widehat A\)
\(\widehat {CDA} = \widehat {AEH}\)
⇒ ∆HAE ᔕ ∆CAD (g.g)
⇒ \(\frac{{HA}}{{CA}} = \frac{{AE}}{{AD}}\)
⇒\(\frac{{HA.HB}}{{CA.CB}} = \frac{{AE.HB}}{{AD.CB}} = \frac{{{S_{AHB}}}}{{{S_{ABC}}}}\)(1)
Tương tự ta có:
\(\frac{{HB.HC}}{{AB.AC}} = \frac{{{S_{AHC}}}}{{{S_{ABC}}}}\)(2)
\(\frac{{HC.HA}}{{BC.BA}} = \frac{{{S_{BHC}}}}{{{S_{ABC}}}}\)(3)
Cộng (1), (2), (3) theo từng vế ta có:
\(\frac{{HA.HB}}{{CA.CB}} + \frac{{HB.HC}}{{AB.AC}} + \frac{{HC.HA}}{{BC.BA}} = \frac{{{S_{AHB}}}}{{{S_{ABC}}}} + \frac{{{S_{AHC}}}}{{{S_{ABC}}}} + \frac{{{S_{BHC}}}}{{{S_{ABC}}}} = 1\)(**)
Từ (*) và (**) ta có: \[{\left( {\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}}} \right)^2} \ge 3\sqrt 1 = 3\]
Hay \(\frac{{HA}}{{BC}} + \frac{{HB}}{{AC}} + \frac{{HC}}{{AB}} \ge \sqrt 3 \).