Câu hỏi:
18/12/2023 126
Cho tam giác ABC . Lấy E là trung điểm của AB và F thuộc cạnh AC sao cho AF = 13AC. Hãy xác định điểm M để →MA+3→MB+2→MC=→0.
Cho tam giác ABC . Lấy E là trung điểm của AB và F thuộc cạnh AC sao cho AF = 13AC. Hãy xác định điểm M để →MA+3→MB+2→MC=→0.
A. M là trung điểm BC;
A. M là trung điểm BC;
B. M là đỉnh hình chữ nhật AEFM;
B. M là đỉnh hình chữ nhật AEFM;
C. M là đỉnh hình bình hành EAFM;
C. M là đỉnh hình bình hành EAFM;
D. M là đỉnh tam giác đều BEM.
D. M là đỉnh tam giác đều BEM.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là C
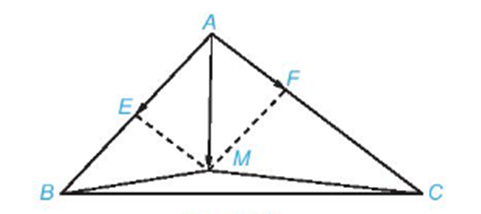
Để xác định vị trí điểm M, trước hết ta biểu thị →AM (với gốc A đã biết) theo hai vec tơ →AB,→AC.
Đẳng thức vec tơ đã cho tương đương với \(\overrightarrow {MA} + 3\left( {\overrightarrow {MA} + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA} + \overrightarrow {AC} } \right) = \overrightarrow 0 \)
⇔6→MA+3→AB+2→AC=→0
⇔→AM=12→AB+13→AC.
Vì E là trung điểm của AB và F thuộc cạnh AC sao cho AF = 13AC nên →AE=12→AB và →AF=13→AC.
Vì vậy →AM=→AE+→AF.
Suy ra M là đỉnh thứ tư của hình bình hành EAFM.
Đáp án đúng là C

Để xác định vị trí điểm M, trước hết ta biểu thị →AM (với gốc A đã biết) theo hai vec tơ →AB,→AC.
Đẳng thức vec tơ đã cho tương đương với \(\overrightarrow {MA} + 3\left( {\overrightarrow {MA} + \overrightarrow {AB} } \right) + 2\left( {\overrightarrow {MA} + \overrightarrow {AC} } \right) = \overrightarrow 0 \)
⇔6→MA+3→AB+2→AC=→0
⇔→AM=12→AB+13→AC.
Vì E là trung điểm của AB và F thuộc cạnh AC sao cho AF = 13AC nên →AE=12→AB và →AF=13→AC.
Vì vậy →AM=→AE+→AF.
Suy ra M là đỉnh thứ tư của hình bình hành EAFM.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Biết rằng hai vectơ →avà →b không cùng phương nhưng hai vectơ 5x→a+4→b và (3x−2)→a−2→bcùng phương. Khi đó giá trị của x bằng:
Biết rằng hai vectơ →avà →b không cùng phương nhưng hai vectơ 5x→a+4→b và (3x−2)→a−2→bcùng phương. Khi đó giá trị của x bằng:
Câu 3:
Chất điểm A chịu tác động của ba lực →F1,→F2,→F3như hình vẽ và ở trạng thái cân bằng (tức là →F1+→F2+→F3=→0). Tính độ lớn của các lực →F2,→F3, biết →F1 có độ lớn là 20N.
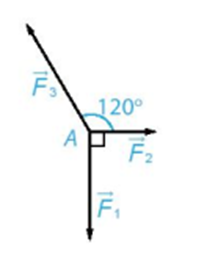
Chất điểm A chịu tác động của ba lực →F1,→F2,→F3như hình vẽ và ở trạng thái cân bằng (tức là →F1+→F2+→F3=→0). Tính độ lớn của các lực →F2,→F3, biết →F1 có độ lớn là 20N.

Câu 4:
Cho tam giác ABC có đường trung tuyến AM. Khi đó →AM=a→AB+b→AC. Tính S = a + 2b.
Cho tam giác ABC có đường trung tuyến AM. Khi đó →AM=a→AB+b→AC. Tính S = a + 2b.
Câu 5:
Cho tam giác ABC có G là trọng tâm tam giác. Hãy xác định điểm M để →MA+→MB+2→MC=→0.
Cho tam giác ABC có G là trọng tâm tam giác. Hãy xác định điểm M để →MA+→MB+2→MC=→0.
Câu 6:
Cho hai vectơ →a và →b khác vec tơ – không. Hai vec tơ nào dưới đây cùng phương?
Cho hai vectơ →a và →b khác vec tơ – không. Hai vec tơ nào dưới đây cùng phương?
Câu 7:
Cho vectơ →a≠→0 với số thực k như thế nào thì vectơ k→a ngược hướng với vectơ →a.
Cho vectơ →a≠→0 với số thực k như thế nào thì vectơ k→a ngược hướng với vectơ →a.
Câu 8:
Các tam giác ABC có trọng tâm G; M, N lần lượt là trung điểm của BC và AB. Biểu thị →MG thông qua hai vec tơ →AB,→AC.
Các tam giác ABC có trọng tâm G; M, N lần lượt là trung điểm của BC và AB. Biểu thị →MG thông qua hai vec tơ →AB,→AC.
Câu 9:
Cho tứ giác ABCD. Gọi M là trung điểm của cạnh AB, CD. Đẳng thức nào dưới đây là sai?
Cho tứ giác ABCD. Gọi M là trung điểm của cạnh AB, CD. Đẳng thức nào dưới đây là sai?
Câu 10:
Cho hai điểm phân biệt A và B. Xác định ví trí điểm K thỏa mãn →KA+2→KB=→0.
Cho hai điểm phân biệt A và B. Xác định ví trí điểm K thỏa mãn →KA+2→KB=→0.
Câu 11:
Cho ba điểm A, B, C phân biệt sao cho →AB=k→AC.Biết rằng C là trung điểm đoạn thẳng AB. Giá trị k thỏa mãn điều kiện nào sau đây?
Cho ba điểm A, B, C phân biệt sao cho →AB=k→AC.Biết rằng C là trung điểm đoạn thẳng AB. Giá trị k thỏa mãn điều kiện nào sau đây?
Câu 12:
Cho vectơ →a, →b và hai số thực k, t. Khẳng định nào sau đây là sai?
Cho vectơ →a, →b và hai số thực k, t. Khẳng định nào sau đây là sai?
Câu 13:
Cho hình vuông ABCD có cạnh AB = 2 và giao điểm các đường chéo là H. Tính độ dài của vectơ →AB+2→AH.
Cho hình vuông ABCD có cạnh AB = 2 và giao điểm các đường chéo là H. Tính độ dài của vectơ →AB+2→AH.
Câu 14:
Trong hình vẽ, hãy biểu thị mỗi vectơ →u,→vhai vectơ →a,→b, tức là tìm các số x, y, z, t để →u=x→a+y→b,→v=t→a+z→b.
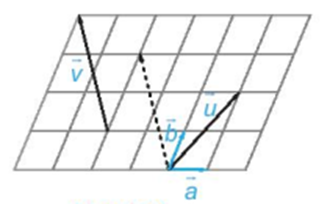
Trong hình vẽ, hãy biểu thị mỗi vectơ →u,→vhai vectơ →a,→b, tức là tìm các số x, y, z, t để →u=x→a+y→b,→v=t→a+z→b.




