Câu hỏi:
19/01/2024 163
Viết phương trình đường tròn tâm I đi qua 3 điểm A(1; 1), B(2; 3) và C(4; 6).
A. x2 + y2 – 5x + y + 26 = 0;
B. x2 + y2 – 4x + 17y + 26 = 0;
C. x2 + y2 – 45x + 17y + 26 = 0;
D. x2 + y2 – 5x + 27y + 56 = 0.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Gọi M, N lần lượt là trung điểm của AB, AC.
Khi đó \(M\left( {\frac{3}{2};2} \right),\,\,N\left( {\frac{5}{2};\frac{7}{2}} \right)\)
Đường trung trực d của đoạn thẳng AB là đường thẳng đi qua M và nhận \(\overrightarrow {AB} = \left( {1;2} \right)\) làm vectơ pháp tuyến nên có phương trình:
\(x - \frac{3}{2} + 2\left( {y - 2} \right) = 0 \Leftrightarrow 2x + 4y - 11 = 0\)
Đường trung trực ∆ của đoạn thẳng AC là đường thẳng đi qua N và nhận \(\overrightarrow {AC} = \left( {3;5} \right)\) làm vectơ pháp tuyến nên có phương trình:
\(3\left( {x - \frac{5}{2}} \right) + 5\left( {y - \frac{7}{2}} \right) = 0 \Leftrightarrow 3x + 5y - 25 = 0\)
Đường thẳng d cắt đường thẳng ∆ cắt nhau tại điểm \(I\left( {\frac{{45}}{2}; - \frac{{17}}{2}} \right)\) cách đều ba điểm A, B, C.
Do đó đường tròn đi qua ba điểm A, B, C có tâm \(I\left( {\frac{{45}}{2}; - \frac{{17}}{2}} \right)\) và bán kính \({R^2} = I{A^2} = {\left( {1 - \frac{{45}}{2}} \right)^2} + {\left( {1 + \frac{{17}}{2}} \right)^2} = \frac{{1105}}{2}\)
Ta có \({\left( {\frac{{45}}{2}} \right)^2} + {\left( { - \frac{{17}}{2}} \right)^2} - \frac{{1105}}{2} = 26\)
Khi đó đường tròn (C) có phương trình là:
x2 + y2 – 45x + 17y + 36 = 0.
Hướng dẫn giải
Đáp án đúng là: C
Gọi M, N lần lượt là trung điểm của AB, AC.
Khi đó \(M\left( {\frac{3}{2};2} \right),\,\,N\left( {\frac{5}{2};\frac{7}{2}} \right)\)
Đường trung trực d của đoạn thẳng AB là đường thẳng đi qua M và nhận \(\overrightarrow {AB} = \left( {1;2} \right)\) làm vectơ pháp tuyến nên có phương trình:
\(x - \frac{3}{2} + 2\left( {y - 2} \right) = 0 \Leftrightarrow 2x + 4y - 11 = 0\)
Đường trung trực ∆ của đoạn thẳng AC là đường thẳng đi qua N và nhận \(\overrightarrow {AC} = \left( {3;5} \right)\) làm vectơ pháp tuyến nên có phương trình:
\(3\left( {x - \frac{5}{2}} \right) + 5\left( {y - \frac{7}{2}} \right) = 0 \Leftrightarrow 3x + 5y - 25 = 0\)
Đường thẳng d cắt đường thẳng ∆ cắt nhau tại điểm \(I\left( {\frac{{45}}{2}; - \frac{{17}}{2}} \right)\) cách đều ba điểm A, B, C.
Do đó đường tròn đi qua ba điểm A, B, C có tâm \(I\left( {\frac{{45}}{2}; - \frac{{17}}{2}} \right)\) và bán kính \({R^2} = I{A^2} = {\left( {1 - \frac{{45}}{2}} \right)^2} + {\left( {1 + \frac{{17}}{2}} \right)^2} = \frac{{1105}}{2}\)
Ta có \({\left( {\frac{{45}}{2}} \right)^2} + {\left( { - \frac{{17}}{2}} \right)^2} - \frac{{1105}}{2} = 26\)
Khi đó đường tròn (C) có phương trình là:
x2 + y2 – 45x + 17y + 36 = 0.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
Câu 2:
Có ba chiếc hộp. Mỗi hộp chứa 5 tấm thẻ được đánh số từ 1 đến 5. Lấy ngẫu nhiên từ mỗi hộp một thẻ rồi cộng các số trên 3 tấm thẻ vừa rút ra lại với nhau. Xác suất để kết quả thu được là số chẵn là:
Câu 3:
Có 5 bưu thiếp khác nhau và 6 bì thư khác nhau. Cần chọn 3 bưu thiếp bỏ vào 3 bì thư, mỗi bì thư một bưu thiếp và gửi cho 3 người bạn mỗi bạn một bưu thiếp. Hỏi có mấy cách thực hiện?
Câu 4:
Xét các số tự nhiên gồm 5 chữ số khác nhau được lập từ các số 1; 3; 5; 7; 9. Xác suất để tìm được một số không có dạng \[\overline {135xy} \] là:
Câu 5:
Trong mặt phẳng Oxy, cho hai điểm A(3; 1) và B(– 2; 4). Viết phương trình đường tròn (C) có tâm I thuộc trục hoành và đi qua hai điểm A, B.
Câu 6:
Hai hộp chứa các quả cầu. Hộp thứ nhất chứa 3 quả đen và 2 quả trắng, hộp thứ hai chứa 4 quả đen và 6 quả trắng.
a) Lấy ngẫu nhiên từ hộp thứ nhất 1 quả. Tính xác suất để lấy được 1 quả đen.
b) Lấy ngẫu nhiên từ mỗi hộp một quả. Tính xác suất để lấy được 2 quả cùng màu.
Hai hộp chứa các quả cầu. Hộp thứ nhất chứa 3 quả đen và 2 quả trắng, hộp thứ hai chứa 4 quả đen và 6 quả trắng.
a) Lấy ngẫu nhiên từ hộp thứ nhất 1 quả. Tính xác suất để lấy được 1 quả đen.
b) Lấy ngẫu nhiên từ mỗi hộp một quả. Tính xác suất để lấy được 2 quả cùng màu.
Câu 8:
Cho 3 hộp, mỗi hộp đựng 5 cái thẻ được đánh số từ 1 đến 5. Rút ngẫu nhiên từ mỗi hộp một tấm thẻ. Biến cố nào sau đây là biến cố chắc chắn?
Câu 10:
Cho kiểu gen AaBb. Giả sử quá trình giảm phân tạo giao tử bình thường và không xảy ra đột biến. Sơ đồ hình cây biểu thị sự hình thành giao tử được biểu diễn như hình bên.
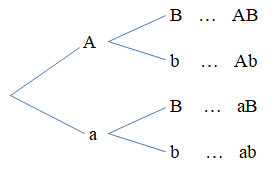
Từ sơ đồ cây, số loại giao tử của kiểu gen AaBb là:
Cho kiểu gen AaBb. Giả sử quá trình giảm phân tạo giao tử bình thường và không xảy ra đột biến. Sơ đồ hình cây biểu thị sự hình thành giao tử được biểu diễn như hình bên.

Từ sơ đồ cây, số loại giao tử của kiểu gen AaBb là:


