Đề kiểm tra giữa học kì 2 Toán 10 Cánh Diều - Đề 01 có đáp án
-
2145 lượt thi
-
38 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Nếu một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có a cách thực hiện, hành động thứ hai có b cách thực hiện (các cách thực hiện của hai hành động là khác nhau đôi một) thì số cách hoàn thành công việc đó là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 2:
Nếu một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có a cách thực hiện, ứng với mỗi cách thực hiện hành động thứ nhất, có b cách thực hiện hành động thứ hai thì số cách hoàn thành công việc đó là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 3:
Một lớp có 31 học sinh nam và 16 học sinh nữ. Có bao nhiêu cách chọn một học sinh làm lớp trưởng của lớp.
 Xem đáp án
Xem đáp án
Đáp án C
Câu 4:
Các thành phố A; B; C; D được nối với nhau bởi các con đường như hình vẽ sau:
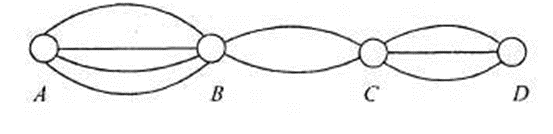
Có bao nhiêu cách đi từ A đến D mà qua B và C chỉ một lần?
 Xem đáp án
Xem đáp án
Đáp án D
Câu 5:
Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Số các chỉnh hợp chập k của n phần tử trên là
 Xem đáp án
Xem đáp án
Đáp án B
Câu 8:
Ở căn hộ chung cư nhà An người ta thường dùng các chữ số từ 0 đến 9 để thiết lập mật khẩu. Nhà An muốn thiết lập một mật khẩu gồm 4 chữ số khác nhau. Số cách thiết lập mật khẩu cho nhà An là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Mỗi mật khẩu nhà bạn An là một chỉnh hợp chập 4 của 10 chữ số.
Vậy có \(A_{10}^4 = 5040\) (cách thiết lập).
Câu 9:
Một tổ có 8 học sinh trong đó có một bạn tên Cường và một bạn tên Nam. Số cách sắp xếp 8 học sinh đó thành một hàng sao cho Cường đứng đầu hàng và Nam đứng cuối hàng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì Cường đứng đầu hàng và Nam đứng cuối hàng nên ta chỉ cần xếp 6 học sinh còn lại. Do đó, có 6! = 720 cách xếp thỏa mãn yêu cầu bài toán.
Câu 11:
Cho k, n là các số nguyên dương với k ≤ n. Trong các phát biểu dưới đây, phát biểu nào sai?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 12:
Cho 8 điểm phân biệt nằm trong mặt phẳng. Hỏi có bao nhiêu đoạn thẳng có hai đầu mút là 2 trong 8 điểm đó?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Các đoạn thẳng được lập không phân biệt điểm đầu và điểm cuối (ví dụ đoạn thẳng AB và đoạn thẳng BA là giống nhau).
Vậy cứ hai điểm phân biệt sẽ cho ta một đoạn thẳng.
Số đoạn thẳng có hai đầu mút là hai trong tám điểm nói trên là số các tổ hợp chập 2 của 8 phần tử. Vậy có tất cả \(C_8^2 = 28\) đoạn thẳng.
Câu 13:
Một tổ có 12 học sinh, trong đó có một học sinh tên Châu. Có bao nhiêu cách chọn một nhóm gồm 5 người trong đó có học sinh tên Châu đi làm trực nhật?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì trong nhóm 5 người được chọn có 1 bạn tên Châu nên 4 bạn còn lại ta sẽ chọn ngẫu nhiên trong 11 người còn lại.
Số cách chọn ngẫu nhiên 4 bạn trong 11 người còn lại là: \(C_{11}^4 = 330\) cách chọn.
Do đó, có 330 cách chọn 5 học sinh trong đó có 1 học sinh tên Châu đi làm trực nhật.
Câu 16:
Hệ số của x3 của khai triển (x – 1)4 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có:
(x – 1)4
= \(C_4^0{x^4} + C_4^1{x^{4 - 1}}.\left( { - 1} \right) + C_4^2{x^{4 - 2}}.{\left( { - 1} \right)^2} + C_4^3{x^{4 - 3}}.{\left( { - 1} \right)^3} + C_4^4.{\left( { - 1} \right)^4}\)
= x4 – 4x3 + 6x2 – 4x + 1.
Do đó, hệ số của x3 là – 4.
Câu 17:
Trong mặt phẳng tọa độ Oxy, cho vectơ \(\overrightarrow a = 3\overrightarrow i - 9\overrightarrow j \). Tọa độ của vectơ \(\overrightarrow a \) là
 Xem đáp án
Xem đáp án
Đáp án C
Câu 18:
Trong mặt phẳng tọa độ Oxy, cho M(2; – 1) và N(4; 1). Tọa độ vectơ \(\overrightarrow {NM} \) là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 19:
Cho hình dưới đây.
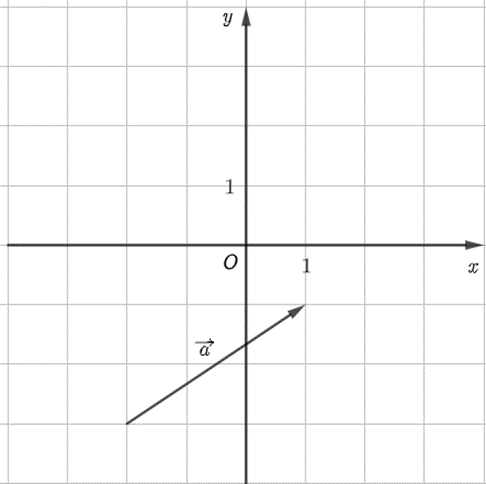
Tọa độ của vectơ \(\overrightarrow a \) trong hình vẽ trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Từ O, dựng vectơ \(\overrightarrow {OA} \) sao cho \(\overrightarrow {OA} = \overrightarrow a \).
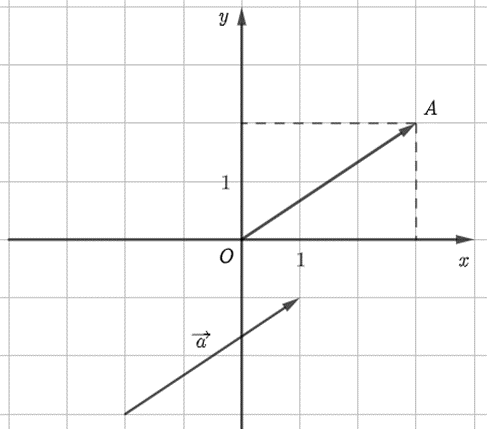
Ta xác định được tọa độ điểm A là (3; 2). Do đó, \(\overrightarrow {OA} = \left( {3;\,\,2} \right)\). Vậy \(\overrightarrow a = \left( {3;\,\,2} \right)\).
Câu 20:
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = \left( { - 5;\,\,3} \right),\,\,\overrightarrow v = \left( {2x + y;\,x - y} \right)\). Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau nếu
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) bằng nhau khi và chỉ khi \(\left\{ \begin{array}{l}2x + y = - 5\\x - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{2}{3}\\y = - \frac{{11}}{3}\end{array} \right.\).
Câu 21:
Cho hình bình hành ABCD có A(– 3; 2), B(– 1; 3), C(– 1; 2). Tọa độ của đỉnh D là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi D(x; y). Ta có \(\overrightarrow {AB} = \left( {2;\,\,1} \right),\,\,\overrightarrow {DC} = \left( { - 1 - x;\,\,2 - y} \right)\).
Vì ABCD là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \)\( \Leftrightarrow \left\{ \begin{array}{l}2 = - 1 - x\\1 = 2 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = 1\end{array} \right.\).
Vậy D(– 3; 1).
Câu 22:
Trong mặt phẳng tọa độ Oxy, cho A(1; 1) và B(5; – 2). Độ dài đoạn thẳng AB là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 23:
Cho ba vectơ \(\overrightarrow x = \left( {1;\, - 2} \right)\), \(\overrightarrow y = \left( {5;\,\,10} \right)\), \(\overrightarrow z = \left( { - \frac{1}{2};\,1} \right)\). Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án B
Câu 24:
Trong mặt phẳng tọa độ Oxy, cho hai vectơ \(\overrightarrow a = \left( {2;\,\, - 1} \right)\) và \(\overrightarrow b = \left( {3;\,\,4} \right)\). Tọa độ của vectơ \(\overrightarrow c = \overrightarrow a + 3\overrightarrow b \) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(\overrightarrow c = \overrightarrow a + 3\overrightarrow b \) = (2; – 1) + 3 . (3; 4) = (2; – 1) + (9; 12) = (2 + 9; – 1 + 12) = (11; 11).
Câu 25:
Số đo góc giữa hai vectơ \(\overrightarrow x = \left( {1;\,\, - 2} \right)\) và \[\overrightarrow y = \left( { - 2;\,\, - 6} \right)\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \(\cos \left( {\overrightarrow x ,\,\overrightarrow y } \right) = \frac{{\overrightarrow x \cdot \overrightarrow y }}{{\left| {\overrightarrow x } \right| \cdot \left| {\overrightarrow y } \right|}} = \frac{{1.\left( { - 2} \right) + \left( { - 2} \right).\left( { - 6} \right)}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 6} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\).
Do đó, \(\left( {\overrightarrow x ,\,\overrightarrow y } \right) = 45^\circ \).
Câu 26:
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 2x – y + 3 = 0. Vectơ pháp tuyến của đường thẳng d là
 Xem đáp án
Xem đáp án
Đáp án C
Câu 28:
Phương trình tham số của đường thẳng ∆ đi qua điểm A(3; 1) và nhận \(\overrightarrow u = \left( {3;\,\, - 1} \right)\) làm vectơ chỉ phương là
 Xem đáp án
Xem đáp án
Đáp án A
Câu 29:
Cho đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right.\). Phương trình tổng quát của đường thẳng d là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng d: \(\left\{ \begin{array}{l}x = 5 + t\\y = - 9 - 2t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = x - 5\\y = - 9 - 2t\end{array} \right.\)⇒ y = – 9 – 2 . (x – 5) ⇔ 2x + y – 1 = 0.
Câu 30:
Cho các điểm A(3; 7) và B(6; 1). Đường thẳng AB có phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \(\overrightarrow {AB} = \left( {3;\,\, - 6} \right)\) là một vectơ chỉ phương của đường thẳng AB.
Do đó \(\overrightarrow u = \frac{1}{3}\overrightarrow {AB} = \left( {1;\,\, - 2} \right)\) cũng là một vectơ chỉ phương của đường thẳng AB.
Suy ra một vectơ pháp tuyến của đường thẳng AB là \(\overrightarrow n = \left( {2;\,\,1} \right)\).
Câu 31:
Cho hai đường thẳng d1: 2x – 3y + 7 = 0 và d2: 4x – 6y + 10 = 0. Chọn khẳng định đúng trong các khẳng định sau.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng d1: 2x – 3y + 7 = 0 có một một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {2;\, - 3} \right)\).
Ta có: 4x – 6y + 10 = 0 ⇔ 2x – 3y + 5 = 0. Do đó, đường thẳng d2 có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {2;\, - 3} \right)\).
Lại có A(– 2; 1) thuộc d1 nhưng không thuộc d2.
Vậy d1 // d2.
Câu 32:
Khoảng cách từ điểm A(1; 1) đến đường thẳng d: 5x – 12y – 6 = 0 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Khoảng cách từ điểm A(1; 1) đến d: 5x – 12y – 6 = 0 là
\(d\left( {A,\,\,d} \right) = \frac{{\left| {5 \cdot 1 - 12 \cdot 1 - 6} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = 1\).
Câu 33:
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng ∆1 và ∆2 có vectơ pháp tuyến lần lượt là \({\vec n_1},\,\,{\vec n_2}\). Nếu \({\vec n_1}.{\vec n_2} = 0\) thì:
 Xem đáp án
Xem đáp án
Đáp án C
Câu 34:
Cho đường thẳng d: x – 2y + 1 = 0. Nếu đường thẳng ∆ đi qua điểm M(1; – 1) và ∆ song song với d thì ∆ có phương trình:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Đường thẳng d có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 2} \right)\).
Vì ∆ // d nên ∆ nhận \({\vec n_d} = \left( {1; - 2} \right)\) làm vectơ pháp tuyến.
Đường thẳng ∆ đi qua M(1; –1) và có vectơ pháp tuyến \({\vec n_d} = \left( {1; - 2} \right)\).
Suy ra phương trình tổng quát của ∆: 1(x – 1) – 2(y + 1) = 0 ⇔ x – 2y – 3 = 0.
Câu 35:
Góc giữa hai đường thẳng a: \(\sqrt 3 \)x – y + 7 = 0 và b: x – \(\sqrt 3 \)y – 2 = 0 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đường thẳng a có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {\sqrt 3 ;\,\, - 1} \right)\);
Đường thẳng b có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {1;\, - \sqrt 3 } \right)\).
Áp dụng công thức tính góc giữa hai đường thẳng ta có:
\(\cos \left( {a,\,\,b} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\,\,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} \cdot \overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right| \cdot \left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {\sqrt 3 \cdot 1 + \left( { - 1} \right) \cdot \left( { - \sqrt 3 } \right)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { - 1} \right)}^2}} \cdot \sqrt {{1^2} + {{\left( { - \sqrt 3 } \right)}^2}} }} = \frac{{\sqrt 3 }}{2}\).
Suy ra góc giữa hai đường thẳng bằng 30°.
Câu 36:
Trong buổi lễ kỉ niệm ngày thành lập Đoàn Thanh niên cộng sản Hồ Chí Minh 26 – 3, bí thư Đoàn trường cần chọn 3 tiết mục từ 7 tiết mục hát và 3 tiết mục từ 6 tiết mục múa rồi xếp thứ tự biểu diễn. Hỏi có bao nhiêu cách chọn và xếp thứ tự sao cho các tiết mục hát và múa xen kẽ nhau?
 Xem đáp án
Xem đáp án
Giả sử các tiết mục được biểu diễn đánh số thứ tự từ 1 đến 6. Vì số lượng tiết mục hát và múa bằng nhau nên có hai trường hợp:
Trường hợp 1: Tiết mục hát diễn ra đầu tiên.
Khi đó, các tiết mục hát có số thứ tự là số lẻ, còn các tiết mục múa có số thứ tự là số chẵn. Như vậy, thứ tự của các tiết mục múa và hát được cố định, chỉ thay đổi thứ tự giữa các tiết mục múa hoặc giữa các tiết mục hát.
Chọn 3 tiết mục từ 7 tiết mục hát và xếp thứ tự có \(A_7^3 = 210\) (cách).
Chọn 3 tiết mục từ 6 tiết mục múa và xếp thứ tự có \(A_6^3 = 120\) (cách).
Khi đó, số cách chọn và xếp thứ tự các tiết mục văn nghệ trong trường hợp tiết mục hát diễn ra đầu tiên là: 210 . 120 = 25 200.
Trường hợp 2. Tiết mục múa diễn ra đầu tiên.
Tương tự, số cách chọn và xếp thứ tự các tiết mục văn nghệ trong trường hợp tiết mục múa diễn ra đầu tiên là: 120 . 210 = 25 200.
Vậy số cách chọn và xếp thứ tự các tiết mục văn nghệ sao cho các tiết mục hát và múa xen kẽ nhau là: 25 200 + 25 200 = 50 400.
Câu 37:
Thực hiện phép tính: \({\left( {\sqrt 7 + \sqrt 5 } \right)^5} - {\left( {\sqrt 7 - \sqrt 5 } \right)^5}\).
 Xem đáp án
Xem đáp án
Ta có: \({\left( {\sqrt 7 + \sqrt 5 } \right)^5} - {\left( {\sqrt 7 - \sqrt 5 } \right)^5}\)
\( = \left[ {{{\left( {\sqrt 7 } \right)}^5} + 5.{{\left( {\sqrt 7 } \right)}^4}.\sqrt 5 + 10.{{\left( {\sqrt 7 } \right)}^3}.{{\left( {\sqrt 5 } \right)}^2} + 10.{{\left( {\sqrt 7 } \right)}^2}.{{\left( {\sqrt 5 } \right)}^3} + 5.\sqrt 7 .{{\left( {\sqrt 5 } \right)}^4} + {{\left( {\sqrt 5 } \right)}^5}} \right]\)
\( - \left[ {{{\left( {\sqrt 7 } \right)}^5} - 5.{{\left( {\sqrt 7 } \right)}^4}.\sqrt 5 + 10.{{\left( {\sqrt 7 } \right)}^3}.{{\left( {\sqrt 5 } \right)}^2} - 10.{{\left( {\sqrt 7 } \right)}^2}.{{\left( {\sqrt 5 } \right)}^3} + 5.\sqrt 7 .{{\left( {\sqrt 5 } \right)}^4} - {{\left( {\sqrt 5 } \right)}^5}} \right]\)
\( = 10.{\left( {\sqrt 7 } \right)^4}.\sqrt 5 + 20.{\left( {\sqrt 7 } \right)^2}.{\left( {\sqrt 5 } \right)^3} + 2.{\left( {\sqrt 5 } \right)^5}\)
\( = 490\sqrt 5 + 700\sqrt 5 + 50\sqrt 5 = 1240\sqrt 5 \).
Câu 38:
Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình \(\left\{ \begin{array}{l}x = 1 + 3t\\y = - 2 - 7t\end{array} \right.\). Đường cao AH có phương trình 2x + 5y + 66 = 0. Viết phương trình đường trung trực của cạnh AB.
 Xem đáp án
Xem đáp án
Ta có A ∈ AM.
Suy ra tọa độ A(1 + 3t; –2 – 7t).
Lại có A ∈ AH.
Suy ra 2(1 + 3t) + 5(–2 – 7t) + 66 = 0.
Do đó –29t + 58 = 0.
Vì vậy –29t = –58.
Khi đó t = 2.
Suy ra tọa độ A(7; –16).
Gọi I là trung điểm của cạnh AB.
Suy ra \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2} = \frac{{7 + 4}}{2} = \frac{{11}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2} = \frac{{ - 16 - 3}}{2} = - \frac{{19}}{2}\end{array} \right.\).
Khi đó tọa độ \(I\left( {\frac{{11}}{2}; - \frac{{19}}{2}} \right)\).
Ta có \(\overrightarrow {AB} = \left( { - 3;13} \right)\).
Đường trung trực d của cạnh AB đi qua điểm \(I\left( {\frac{{11}}{2}; - \frac{{19}}{2}} \right)\) và có vectơ pháp tuyến \(\overrightarrow {AB} = \left( { - 3;13} \right)\).
Suy ra phương trình d: \( - 3\left( {x - \frac{{11}}{2}} \right) + 13\left( {y + \frac{{19}}{2}} \right) = 0\) ⇔ 3x – 13y – 140 = 0.
