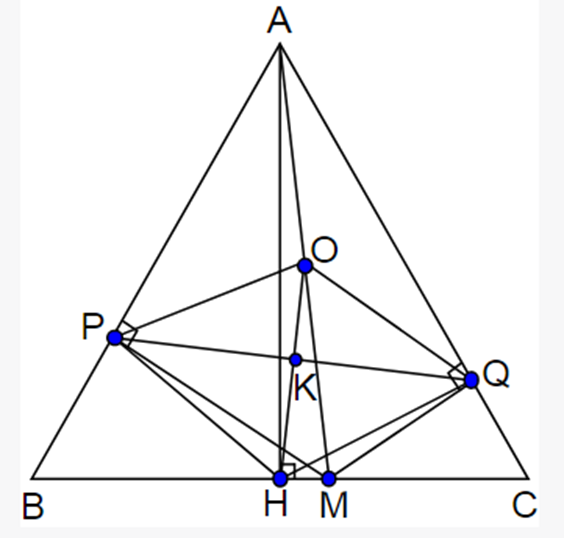
Xét \(\Delta APM\)vuông tại P ta có PO là đường trung tuyến ứng với cạnh huyền AM.

→ OA = OP = OM.

Tương tự cho \[\Delta AHM\]vuông tại H và \(\Delta AQM\)vuông tại Q ta có:

OA = OP = OH = OM = OQ    (1)

→ \(\Delta AOP\)và \[\Delta AOH\]cân tại O.

Xét \(\Delta ABC\)đều ta có:

AH là đường cao cũng là đường phân giác 

\[ \Rightarrow \widehat {{\rm{BAH}}}{\rm{ = }}\frac{{\rm{1}}}{{\rm{2}}}\widehat {{\rm{BAC}}}{\rm{ = 3}}{{\rm{0}}^{\rm{0}}}\]

Ta có:

\[\widehat {{\rm{POM}}}{\rm{ = 2 }}\widehat {{\rm{PAO}}}\] ( góc ngoài của \(\Delta AOP\)cân tại O)

\[\widehat {{\rm{HOM}}}{\rm{\; = 2}}\widehat {{\rm{HAO}}}\] ( góc ngoài của \(\Delta AOH\)cân tại O)

\[ \Rightarrow {\rm{ }}\widehat {{\rm{POM}}}{\rm{ - }}\widehat {{\rm{HOM}}}{\rm{ = 2}}\left( {{\rm{ }}\widehat {{\rm{PAO}}}{\rm{ -   }}\widehat {{\rm{HAO}}}} \right)\]

\[ \Rightarrow {\rm{ }}\widehat {{\rm{POH}}}{\rm{ = 2}}\widehat {{\rm{PAH}}}\]

Mà\[{\rm{ }}\widehat {{\rm{PAH}}}{\rm{ = 3}}{{\rm{0}}^{\rm{0}}}\]( cmt)  

Nên \[\widehat {{\rm{POH}}}{\rm{ = 6}}{{\rm{0}}^{\rm{0}}}\]

Mặt khác OH = OP ( cmt)

\[ \Rightarrow {\rm{ \Delta POH}}\]đều.

→ PH = OP    (2)

Tương tự ta có \[\Delta QOH\]đều 

→ QH = OQ    (3)

Từ (1), (2), (3) suy ra OP = OQ = PH = HQ

→ Tứ giác OPHQ là hình thoi ( tứ giác có 4 cạnh bằng nhau)

 Gọi K là giao điểm của OH và PQ.

Do tứ giác OPHQ là hình thoi và K là giao điểm 2 đường chéo OH và PQ

Nên K là trung điểm của OH và PQ và \[{\rm{OH }} \bot {\rm{ PQ}}\]tại K.

\[ \Rightarrow {\rm{ OK = }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{OH = }}\frac{{\rm{1}}}{{\rm{4}}}{\rm{AM}}\].

Xét \[\Delta OKP\]vuông tại K theo định lý Pitago thuận ta có:

\[{\rm{P}}{{\rm{K}}^{\rm{2}}}{\rm{\; = O}}{{\rm{P}}^{\rm{2}}}{\rm{\; - O}}{{\rm{K}}^{\rm{2}}}{\rm{\; = }}\frac{1}{4}{\rm{ A}}{{\rm{M}}^{\rm{2}}}{\rm{\; - }}\frac{1}{{16}}{\rm{ A}}{{\rm{M}}^{\rm{2}}}{\rm{\; = }}\frac{3}{{16}}{\rm{ A}}{{\rm{M}}^{\rm{2}}}\]

\( \Rightarrow {\rm{PK = }}\frac{{\sqrt {\rm{3}} }}{{\rm{4}}}{\rm{AM}}\)

\( \Rightarrow {\rm{PQ = }}\frac{{\sqrt {\rm{3}} }}{{\rm{2}}}{\rm{AM}}\)

→ PQ nhỏ nhất khi AM nhỏ nhất.

Mà AM nhỏ nhất khi AM = AH

→ M trùng với H thì PQ nhỏ nhất.