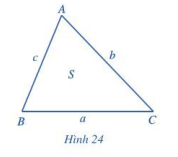
Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24)
1k
09/06/2023
Hoạt động 5 trang 75 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24).
a) Từ định lí côsin, chứng tỏ rằng:
sinA=2bc√p(p−a)(p−b)(p−c), ở đó p=a+b+c2.
b) Bằng cách sử dụng công thức S=12bcsinA, hãy chứng tỏ rằng:
S=√p(p−a)(p−b)(p−c).
Trả lời
a) Xét tam giác ABC, ta có:
BC2 = AB2 + AC2 - 2.AB.AC.cos A (định lí cosin)
⇒ cos A = AB2+AC2−BC22.AB.AC
⇒ cos A = c2+b2−a22.c.b
⇒cos2A=(b2+c2−a2)24b2c2
Do ˆA là góc của tam giác ABC nên 0°.
Do đó sin A > 0.
Lại có cos2 A + sin2 A = 1 nên sin2 A = 1 - cos2 A.
mà
Do sin A > 0 nên .
Do đó .
b) Ta có diện tích tam giác ABC: S = bc.sin A.
Mà nên S = bc. .
Do đó .
Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:
Bài tập cuối chương 3
Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác
Bài 2: Giải tam giác. Tính diện tích tam giác
Bài 3: Khái niệm vectơ
Bài 4: Tổng và hiệu của hai vectơ
Bài 5: Tích của một số với một vectơ

