Cho (O; R) và (O’; R’) tiếp xúc ngoài tại A. Kẻ dây cung AM của (O) và dây cung AN của (O’) sao cho AM vuông góc với AN.
a) Chứng minh OM // O’N.
b) Xác định vị trí của AM và AN để diện tích tứ giác OMNO’ lớn nhất.
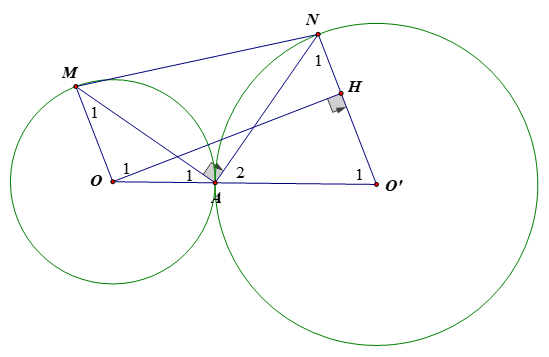
a) • Vì OM = OA = R nên tam giác OMA cân tại O.
Do đó \[{\widehat {O'}_1} = 180^\circ - 2.{\widehat A_1}\].
• Vì O’N = O’A = R’ nên tam giác O’NA cân tại O’.
Do đó \[{\widehat {O'}_1} = 180^\circ - 2.{\widehat A_2}\].
Lại có: \({\widehat A_1} + {\widehat A_2} + \widehat {MAN} = 180^\circ \) mà \(\widehat {MAN} = 90^\circ \).
Suy ra \({\widehat A_1} + {\widehat A_2} = 90^\circ \)
Ta có \({\widehat O_1} + {\widehat {O'}_1} = 180^\circ - 2.{\widehat A_1} + 180^\circ - 2.{\widehat A_2}\)
\( = 360^\circ - 2.\left( {{{\widehat A}_1} + {{\widehat A}_2}} \right)\)\( = 360^\circ - 2.90^\circ = 180^\circ \).
Mà đây là cặp góc trong cùng phía bù nhau.
Do đó OM // O’N.
b) Gọi H là hình chiếu vuông góc của O lên O’N.
Vì OM // O’N nên tứ giác OMNO’ là hình thang.
Do đó \({S_{OMNO'}} = \frac{{\left( {OM + O'N} \right).OH}}{2}\)\( = \frac{{\left( {R + R'} \right).OH}}{2}\)
\( \le \frac{{\left( {R + R'} \right).OO'}}{2}\)\( = \frac{{\left( {R + R'} \right).\left( {R + R'} \right)}}{2}\)\( = \frac{{{{\left( {R + R'} \right)}^2}}}{2}\).
Dấu “=” xảy ra khi H ≡ O’ hay OO’ vuông góc với O’N, OO’ vuông góc OM.