Cho nửa đường tròn (O) đường kính AB. M là trung điểm OA. N là điểm bất kỳ thuộc nửa đường tròn. Qua N kẻ đường thẳng vuông góc với MN cắt các tiếp tuyến tại A và B tại C và D. Tìm vị trí của N để diện tích tam giác DMC min.
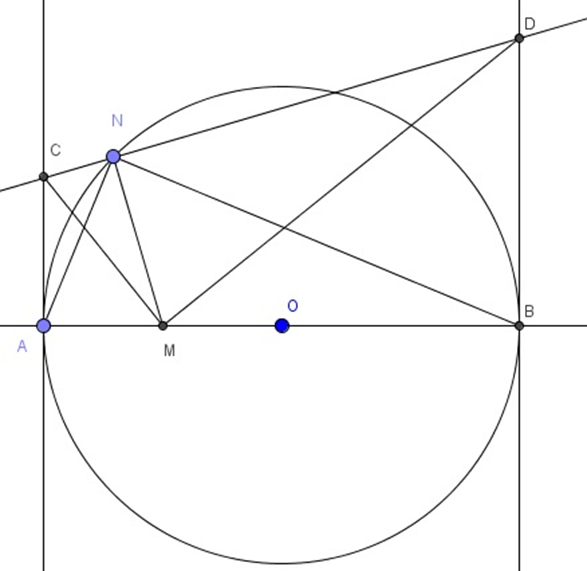
Tứ giác AMNC có \(\widehat {MAC} + \widehat {MNC} = 90^\circ + 90^\circ = 180^\circ \) nên tứ giác AMNC là tứ giác nội tiếp đường tròn
Khi đó \(\widehat {CNM} = \widehat {CMA}\) (Hai góc cùng chắn cung CA)
Chứng minh tương tự ta được MBDN là tứ giác nội tiếp nên suy ra
\(\widehat {DNB} = \widehat {DMB}\) (Hai góc cùng chắn cung DB)
Suy ra \(\widehat {CNM} + \widehat {DNB} = \widehat {CMA} + \widehat {DMB}\)
\( \Rightarrow 180^\circ - \left( {\widehat {CNM} + \widehat {DNB}} \right) = 180^\circ - \left( {\widehat {CMA} + \widehat {DMB}} \right)\)
\( \Rightarrow \widehat {ANB} = \widehat {CMD} \Rightarrow \widehat {CMD} = 90^\circ \Rightarrow CM \bot DM\)
Suy ra \[\widehat {CMA} + \widehat {DMB} = 90^\circ \]
Mà \[\widehat {CMA} + \widehat {ACM} = 90^\circ \]
Do đó \(\widehat {ACM} = \widehat {BMD}\)
Xét ∆ACM và ∆BMD có:
\(\widehat {ACM} = \widehat {BMD}\) (cmt)
\(\widehat {CAM} = \widehat {MBD} = 90^\circ \)
Suy ra ∆ACM ᔕ ∆BMD (g.g)
\( \Rightarrow \frac{{AM}}{{BD}} = \frac{{AC}}{{BM}} \Rightarrow AM\,.\,BM = BD\,.\,AC\) (không đổi)
Theo Bunhiacopxki, ta có:
(AM.BM + AC.BD)2 ≤ (AM2 + AC2)(BM2 + BD2) = MC2.MD2 = 4(SDMC)2
Þ SDMC đạt giá trị nhỏ nhất khi AC = AM, BD = BM