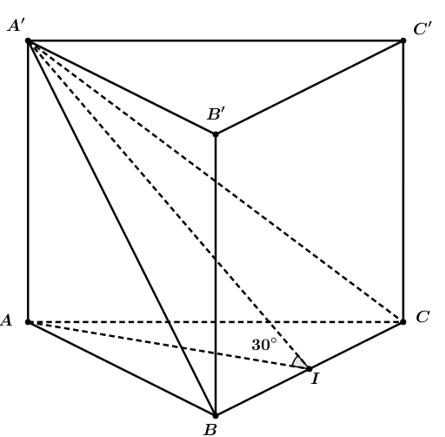
Cho lăng trụ tam giác ABCA'B'C' có BB'=a, góc giữa đường thẳng BB' và (ABC) bằng $60°$  , tam giác  ABC vuông tại C và góc $\widehat{BAC}=60°$. Hình chiếu vuông góc của điểm B' lên (ABC) trùng với trọng tâm của$\Delta ABC$ . Thể tích của khối tứ diện theo $A^{\text{'}}.ABC$  bằng a

Lời giải

Chọn D

Gọi G  là trọng tâm $\Delta ABC$  .

 $\Rightarrow B^{\text{'}}G\perp \left(ABC\right)$.

là hình chiếu của $B{B}^{\text{'}}$  lên $\left(ABC\right)$ .

$\Rightarrow \left(\widehat{B{B}^{\text{'}},\left(ABC\right)}\right)=\left(\widehat{B{B}^{\text{'}},BG}\right)=\widehat{B^{\text{'}}GB}=60°$ (vì $\Delta B{B}^{\text{'}}G$  vuông tại G  nên $\widehat{B^{\text{'}}GB}$  nhọn).

$\Rightarrow B^{\text{'}}G=B{B}^{\text{'}}.\sin 60°=\frac{a\sqrt{3}}{2}$ ; $BG=B{B}^{\text{'}}.\cos 60°=\frac{a}{2}$ .

Gọi $\Delta ABC$  là trung điểm AC .

Lại có : $\Delta ABC$  vuông tại C  và góc $\widehat{BAC}=60°$$\Rightarrow BC=AC.\tan 60°=AC.\sqrt{3}$ .

$\Delta BCM$ vuông tại C$\Rightarrow B{C}^2+M{C}^2=B{M}^2\iff 3A{C}^2+\frac{A{C}^2}{4}=\frac{9a^2}{16}\iff AC=\frac{3a\sqrt{13}}{26}$  .

 $\Rightarrow BC=\frac{3a\sqrt{39}}{26}\Rightarrow S_{\Delta ABC}=\frac{1}{2}BC.AC=\frac{9a^2\sqrt{3}}{104}$   .

$\left(ABC\right)\text{//}\left(A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}\right)\Rightarrow d\left(A^{\text{'}},\left(ABC\right)\right)=d\left(B^{\text{'}},\left(ABC\right)\right)=B^{\text{'}}G=\frac{a\sqrt{3}}{2}$.

Thể tích của khối tứ diện $A^{\text{'}}.ABC$  : $V_{A^{\text{'}}.ABC}=\frac{1}{3}.B^{\text{'}}G.S_{\Delta ABC}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.\frac{9a^2\sqrt{3}}{104}=\frac{9a^3}{208}$ .