Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của AB, CD

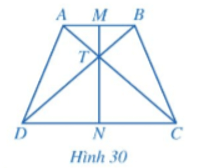
Bài 1 trang 103 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của AB, CD và T là giao điểm của AC và BD (Hình 30).

Chứng minh:

a) $\widehat{TAD}=\widehat{TBC},\widehat{TDA}=\widehat{TCB}$;

b) TA = TB, TD = TC;

c) MN là đường trung trực của cả hai đoạn thẳng AB và CD.

Trả lời

a) Do ABCD là hình thang cân nên AC = BD và AD = BC (tính chất hình thang cân).

Xét ΔADC và ΔBCD có:

AD = BC; AC = BD; DC là cạnh chung

Do đó ΔADC = ΔBCD (c.c.c)

Suy ra $\widehat{CAD}=\widehat{DBC}$ (hai góc tương ứng)

Hay $\widehat{TAD}=\widehat{TBC}$.

Chứng minh tương tự ta cũng có: ΔABD = ΔBAC (c.c.c)

Suy ra $\widehat{BDA}=\widehat{ACB}$ (hai góc tương ứng)

Hay $\widehat{TDA}=\widehat{TCB}$.

b) Xét ΔTAD và ΔTBC có:

$\widehat{TAD}=\widehat{TBC}$; AD = BC; $\widehat{TDA}=\widehat{TCB}$.

Do đó ΔTAD = ΔTBC (g.c.g).

Suy ra TA = IB và TD = TC (các cặp cạnh tương ứng).

c) • Do TA = TB nên tam giác TAB cân tại T.

ΔTAB cân tại T có TM vừa là đường trung tuyến vừa là đường cao do đó TM là đường trung trực của đoạn thẳng AB nên TM ⊥ AB.

• Do TD = TC nên tam giác TCD cân tại T.

ΔTCD cân tại T có TN vừa là đường trung tuyến vừa là đường cao do đó TN là đường trung trực của đoạn thẳng CD nên TN ⊥ CD.

• Do AB // CD, TM ⊥ AB, TN ⊥ CD nên T, M, N thẳng hàng

Hay MN là đường trung trực của cả hai đoạn thẳng AB và CD.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 1: Định lí Pythagore

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành