Cho hình nón đỉnh S có chiều cao h = 5a, bán kính đáy r = 7a. Một thiết diện đi qua đỉnh của hình nón và có khoảng cách từ tâm O của đáy đến mặt phẳng chứa thiết diện là 4a. Tính diện tích của thiết diện đó.

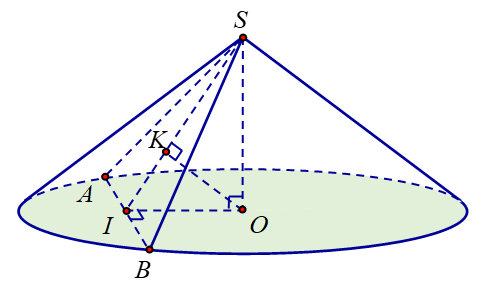
Giả sử thiết diện SAB đi qua đỉnh S cắt đường tròn đáy tại A và B (như hình vẽ).
Gọi I là trung điểm của dây cung AB. Từ tâm O của đáy vẽ $OK\perp SI$ thì $OK\perp \left(SAB\right)$.
Theo bài ra ta có $AO=r=7a$; $SO=h=5a$; $OK=4a$.
Trong tam giác vuông SOI ta có:
$$\begin{gathered} \frac{1}{O{K}^2}=\frac{1}{O{I}^2}+\frac{1}{O{S}^2}\Rightarrow OI=\frac{OS.OK}{\sqrt{O{S}^2-O{K}^2}}=\frac{5a.4a}{\sqrt{25a^2-16a^2}}=\frac{20a}{3} \\ SI=\sqrt{S{O}^2+O{I}^2}=\sqrt{25a^2+\frac{400a^2}{9}}=\frac{25a}{3} \end{gathered}$$
Xét tam giác vuông OAI ta có: $AB=2AI=2\sqrt{A{O}^2-O{I}^2}=2\sqrt{49a^2-\frac{400a^2}{9}}=\frac{2a\sqrt{41}}{3}$.
Vậy diện tích của thiết diện SAB là $S_{\Delta SAB}=\frac{1}{2}.\frac{25a}{3}.\frac{2a\sqrt{41}}{3}=\frac{25a^2\sqrt{41}}{9}.$