Cho hình nón chứa bốn mặt cầu cùng có bán kính là $\sqrt{2},$  trong đó ba mặt cầu tiếp xúc với đáy, tiếp xúc lẫn nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ tư tiếp xúc với ba mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón. Tính bán kính đáy của hình nón.

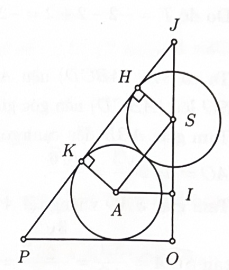
Xét trường hợp tổng quát là bốn mặt cầu có bán kính r.
Gọi tâm các mặt cầu là S, A, B, C, trong đó S là tâm của mặt cầu trền cùng. Do các mặt cầu tiếp xúc ngoài nhau nên S.ABC là chóp đều cạnh 2r.

Gọi I là tâm của tam giác ABC, khi đó SI vuông góc với mặt phẳng $\left(ABC\right)$ và $AI=\frac{2r\sqrt{3}}{3}.$
Tam giác SAI$ vuông tại I, có $SI=\sqrt{S{A}^2-A{I}^2}=\sqrt{4r^2-{\left(\frac{2r\sqrt{3}}{3}\right)}^2}=\frac{2r\sqrt{6}}{3}.$
Kẻ đường sinh JP của hình nón tiếp xúc với hai mặt cầu tâm S và tâm A lần lượt tại H, K.
Ta có $\Delta SAI~\Delta JSH$ (g-g) nên $\frac{SJ}{SA}=\frac{SH}{AI}$$\Rightarrow SJ=\frac{SA.SH}{AI}=2r.r.\frac{3}{2r\sqrt{3}}=r\sqrt{3}.$
Chiều cao của khối nón là
$h=JS+SI+IO=r\sqrt{3}+\frac{2r\sqrt{6}}{3}+r=r\left(1+\sqrt{3}+\frac{2\sqrt{6}}{3}\right)$
Bán kính khối nón là $R=OP=JO.\tan \widehat{SJH}$
$\iff R=h.\tan ASI=r\left(1+\sqrt{3}+\frac{2\sqrt{6}}{3}\right).\frac{AI}{SI}$
$=r\left(1+\sqrt{3}+\frac{2\sqrt{6}}{3}\right)\frac{2r\sqrt{3}}{3}\cdot \frac{3}{2r\sqrt{6}}=r\left(1+\sqrt{3}+\frac{2\sqrt{6}}{3}\right)\frac{1}{\sqrt{2}}.$
Áp dụng với $r=\sqrt{2}$ ta được $R=\sqrt{2}.\frac{1}{\sqrt{2}}.\left(1+\sqrt{3}+\frac{2\sqrt{6}}{3}\right)=1+\sqrt{3}+\frac{2\sqrt{6}}{3}.$

Chọn C