Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng: vectơ OA + OB + OC + OD + OE = 0
Bài 5 trang 103 SBT Toán 10 Tập 1: Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng: →OA+→OB+→OC+→OD+→OE=→0.
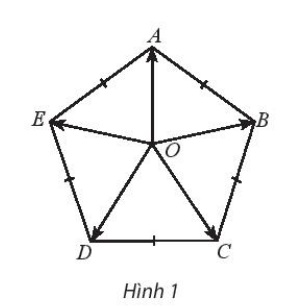
Bài 5 trang 103 SBT Toán 10 Tập 1: Cho hình ngũ giác đều ABCDE tâm O. Chứng minh rằng: →OA+→OB+→OC+→OD+→OE=→0.

Đặt →u = →OA+→OB+→OC+→OD+→OE
Ta có: →u = →OA+(→OB+→OE)+(→OC+→OD)
Do OA nằm trên đường phân giác của ^BOE và ^DOC của hai tam giác cân BOE và DOC nên ta có các vectơ (→OB+→OE) và (→OC+→OD) nằm trên đường thẳng OA, suy ra →u nằm trên đường thẳng OA.
Chứng minh tương tự ta có →u cũng đồng thời nằm trên đường thẳng OB. Như vậy →u = →0
Vậy ![]()
Xem thêm các bài giải SBT Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Tích của một số với một vectơ
Bài 4: Tích vô hướng của hai vectơ