Giải Sách bài tập Toán 10 Bài 4: Tích vô hướng của hai vectơ
Giải SBT Toán 10 trang 100 Tập 1
Bài 1 trang 100 SBT Toán 10 Tập 1: Cho tam giác vuông cân ABC có AB = AC = a.
Tính các tích vô hướng →AB.→AC, →AC.→CB.
Lời giải:
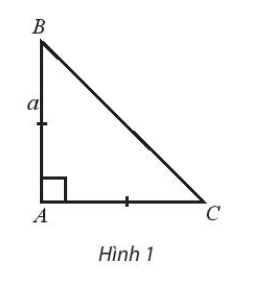
Do tam giác ABC vuông tại A nên AB ⊥ AC ⇒ →AB.→AC = 0;
Ta có: ![]()
Tam giác ABC vuông cân tại A nên ^ACB = 45°
Như vậy:
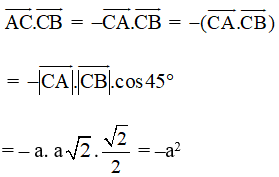
Vậy →AB.→AC = 0 và →AC.→CB= –a2.
Bài 2 trang 100 SBT Toán 10 Tập 1: Cho hình chữ nhật ABCD có tâm O và AD = 2a, AB = a. Tính:
a) →AB.→AO;
b) →AB.→AD.
Lời giải:
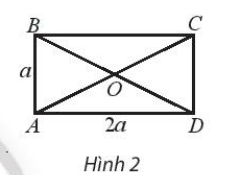
a) Vì ABCD là hình chữ nhật nên AB = CD = a, AD = BC = 2a.
Ta có: AC = √AB2+BC2 = √a2+(2a)2 = a√5.
Xét tam giác BAC vuông tại B, có: cos^BAO = cos^BAC= ABAC=a√5a=1√5.
ABCD là hình chữ nhật nên O là trung điểm của AC và BD
⇒ AO = 12AC = a√52.
→AB.→AO = |→AB|.|→AO|. cos^BAO =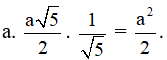
Vậy 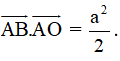
b) Do ABCD là hình chữ nhật nên ![]()
Giải SBT Toán 10 trang 101 Tập 1
a) Chứng minh![]()
b) Tính ![]() theo R.
theo R.
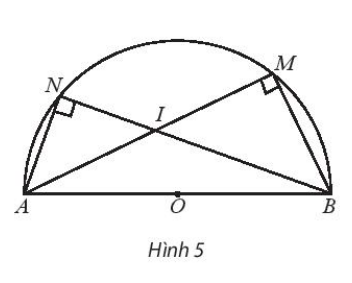
Lời giải:
a) AB là đường kính nên ^AMB = ^ANB = 90° ( góc nội tiếp chắn nửa đường tròn ).
AM ⊥ MB và AN ⊥ NB.
Ta có:
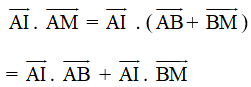
Mà AI ⊥ BM do AM ⊥ MB nên ![]()
Như vậy ![]()
Tương tự ta có:
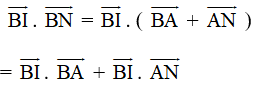
Mà BI ⊥ AN do AN ⊥ NB nên ![]()
Như vậy ![]()
b) Ta có:
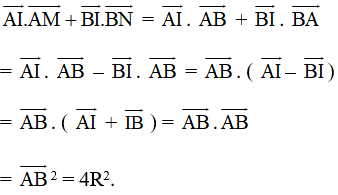
Lời giải:
Áp dụng công thức tính công ta có:
![]() = 60.200.cos60° = 6000 (J).
= 60.200.cos60° = 6000 (J).
Vậy công sinh bởi lực →F bằng 6000 J.
Lời giải:
Gọi hai vectơ lần lượt là →v1, →v2 và góc giữa hai vectơ là α.
Ta có ![]() = 6.8.cos α = 24
= 6.8.cos α = 24 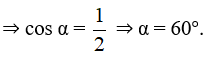
Vậy góc giữa hai vectơ đề cho là 60°.
Xem thêm lời giải sách bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 2: Tổng và hiệu của hai vectơ




