Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính khoảng cách : a) Giữa hai mặt phẳng

Thực hành 2 trang 77 Toán 11 Tập 2: Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính khoảng cách :

a) Giữa hai mặt phẳng (ACD′) và (A′C′B) ;

b) Giữa đường thẳng AB và (A′B′C′D′).

Trả lời

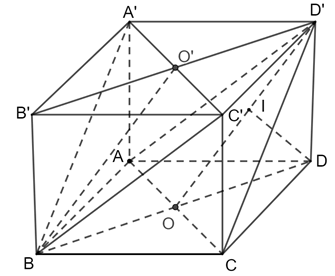
a) Ta có $\left({\mathrm{ACD}}^{\text{'}}\right)\text{//}\left({\mathrm{BA}}^{\text{'}}{C}^{\text{'}}\right)$

$\text{⇒ d}\left(\left({\mathrm{ACD}}^{\text{'}}\right),\left({\mathrm{BA}}^{\text{'}}{C}^{\text{'}}\right)\right)=d\left(B,\left({\mathrm{ACD}}^{\text{'}}\right)\right)=d\left(D,\left({\mathrm{ACD}}^{\text{'}}\right)\right)$

Gọi I là hình chiếu vuông góc của D trên OD′.

Ta có $\left\{\begin{array}{l}\mathrm{AC}\perp \mathrm{BD}\\ \mathrm{DD}\text{'}\perp \left(\mathrm{ABCD}\right)\end{array}\right.\Rightarrow \left\{\begin{array}{l}\mathrm{AC}\perp \mathrm{BD}\\ \mathrm{DD}\text{'}\perp \mathrm{AC}\end{array}\right.$

$\Rightarrow \mathrm{AC}\perp \left({\mathrm{BDD}}^{\text{'}}{B}^{\text{'}}\right)\Rightarrow \mathrm{AC}\perp \mathrm{DI}$ và $\mathrm{DI}\perp {\mathrm{OD}}^{\text{'}}$

$\Rightarrow \mathrm{DI}\perp \left(D^{\text{'}}\mathrm{AC}\right)\Rightarrow d\left(D,\left(D^{\text{'}}\mathrm{AC}\right)\right)=\mathrm{DI}$

• Xét tam giác ABD vuông tại A nên ta có:

$\mathrm{BD}=\sqrt{{\mathrm{AB}}^2+{\mathrm{AD}}^2}=a\sqrt{2}\Rightarrow \mathrm{OD}=\frac{a\sqrt{2}}{2}.$

• Xét tam giác D′DO vuông tại D có DI là đường cao nên

$\frac{1}{{\mathrm{DI}}^2}=\frac{1}{{\mathrm{OD}}^2}+\frac{1}{D{D^{\text{'}}}^2}=\frac{2}{a^2}+\frac{1}{a^2}=\frac{3}{a^2}$

$\Rightarrow d\left(\left({\mathrm{ACD}}^{\text{'}}\right),\left(A^{\text{'}}{C}^{\text{'}}B\right)\right)=\mathrm{DI}=\frac{a\sqrt{3}}{3}.$

b) Ta có: AB // (A′B′C′D′).

Do đó d(AB, (A′B′C′D′)) = AA′ = a

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: