Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = SB = SC = SD = a căn 2

Bài 3 trang 81 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $\mathrm{SA}=\mathrm{SB}=\mathrm{SC}=\mathrm{SD}=a\sqrt{2}$ . Gọi I, J lần lượt là trung điểm của AB và CD.

a) Chứng minh AB ⊥ (SIJ).

b) Tính khoảng cách giữa hai đường thẳng AB và SC.

Trả lời

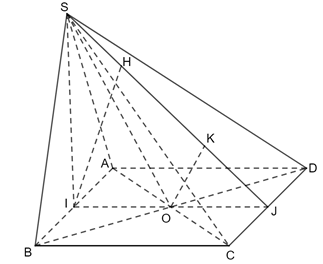
a) Ta có: ΔSAB cân tại S và đáy là hình vuông ABCD.

$\Rightarrow \left\{\begin{array}{l}\mathrm{SI}\perp \mathrm{AB}\\ \mathrm{IJ}\perp \mathrm{AB}\end{array}\right.\Rightarrow \mathrm{AB}\perp \left(\mathrm{SIJ}\right).$

b) Ta có: AB // CD ⇒ AB // (ABCD)

$\Rightarrow$ d(AB, SC) = d(AB, (SCD)) = d(I, (SCD))

Gọi H, K lần lượt là hình chiếu vuông góc của I, O trên SJ

Ta có $\left\{\begin{array}{l}\mathrm{IH}//\mathrm{OK}\\ \mathrm{IH}=2\text{O}\mathrm{K}\end{array}\right.$

Vì AB // CD nên CD ⊥ (SIJ) $\Rightarrow$ CD ⊥ IH $\Rightarrow$IH ⊥ (SCD)

$\Rightarrow$ d(AB, CD) = d(AB, (SCD)) = IH = 2OK

Ta có: ABCD là hình vuông

$\Rightarrow$ $\mathrm{OA}=\frac{\mathrm{AC}}{2}=\frac{\sqrt{{\mathrm{AD}}^2+{\mathrm{CD}}^2}}{2}=\frac{a\sqrt{2}}{2}$

• Xét ΔSAO vuông tại O có

$\mathrm{SO}=\sqrt{{\mathrm{SA}}^2-{\mathrm{OA}}^2}=\frac{a\sqrt{6}}{2}.$

• Xét ΔSOJ vuông tại O có đường cao OK nên

$\mathrm{OK}=\frac{\mathrm{SO}.\text{OJ}}{\sqrt{{\mathrm{SO}}^2+{\mathrm{OJ}}^2}}=\frac{a\sqrt{42}}{14}$

Do đó $d\left(\mathrm{AB},\mathrm{SC}\right)=2\text{O}K=\frac{a\sqrt{42}}{7}$.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: