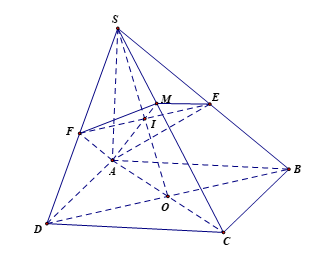
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Biết SA ^ (ABCD) và $SA=\text{a}\sqrt{2}$ . Mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng SC, cắt các cạnh SC, SB, SD lần lượt tại M, E, F.

a) Chứng minh AE ^ (SBC).

a) Gọi O là giao điểm của AC và BD. Kẻ AM ^ SC tại M, SO Ç AM = I.

Do ABCD là hình vuông nên AC ^ BD.

Vì SA ^ (ABCD) nên SA ^ BD mà AC ^ BD nên BD ^ (SAC), suy ra BD ^ SC.

Trong mặt phẳng (SBD), qua I kẻ đường thẳng song song với BD cắt SB, SD lần lượt tại E và F. Khi đó (P) = (AEMF).

Do ABCD là hình vuông nên BC ^ AB, SA ^ BC (do SA ^ (ABCD)) nên BC ^ (SAB), suy ra BC ^ AE.

Mặt khác SC ^ (P) nên SC ^ AE mà BC ^ AE nên AE ^ (SBC).