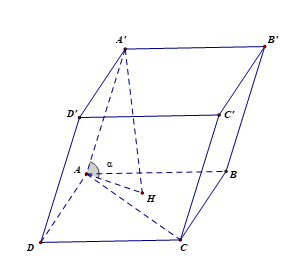
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật. Biết AC = AA' = 2a. Giá trị lớn nhất của thể tích hình hộp ABCD.A'B'C'D' bằng

Xét tam giác ABC vuông tại B, có AC² = AB² + BC².

Ta có S_ABCD = AB × BC ≤$\frac{A{B}^2+B{C}^2}{2}=\frac{A{C}^2}{2}=2a^2$ . Dấu “=” xảy ra khi AB = BC.

Gọi H là hình chiếu của A' trên mặt phẳng (ABCD). Khi đó A'H ^ (ABCD). Khi đó AH là hình chiếu của AA' trên mặt phẳng (ABCD).

Gọi a là góc tạo bởi đường thẳng AA' và mặt phẳng (ABCD). Khi đó .

Xét tam giác A'AH vuông tại H có A'H = AA' × sina ≤ AA' = 2a.

Dấu bằng xảy ra khi a = 90° hay AA' ^ (ABCD).

Do đó V_{ABCD.A'B'C'D'} = S_ABCD × A'H ≤ 2a² × 2a = 4a³.

Vậy giá trị lớn nhất của thể tích hình hộp ABCD.A'B'C'D' bằng 4a³.