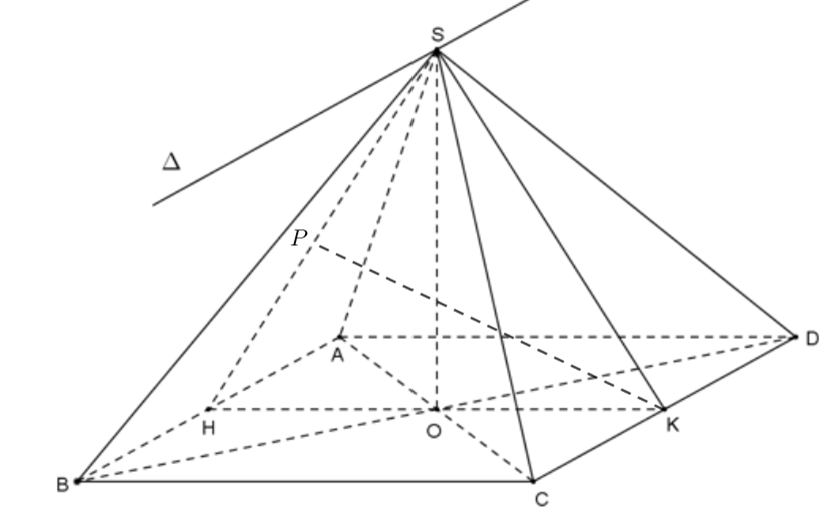
Cho hình chóp tứ giác đều S.ABCD có góc giữa hai mặt phẳng (SAB) và (SCD) bằng 60o và khoảng cách giữa hai đường thẳng SA và CD bằng a. Tính thể tích V của khối chóp S.ABCD theo a.

A. $V=\frac{2a^3}{9}$

B. $V=\frac{4a^3}{9}$

C. $a^3\sqrt{3}$

D. $V=\frac{2a^3\sqrt{3}}{3}$

Trả lời

Chọn B

Gọi O là tâm của hình vuông ABCD.

Do S.ABCD là hình chóp đều nên $SO\perp \left(ABCD\right)\Rightarrow SO\perp AB$.

Ta có: S là một điểm chung của hai mặt phẳng (SAB) và (SCD).

$AB\subset \left(SAB\right); CD\subset \left(SCD\right); AB//CD$.

Suy ra hai mặt phẳng (SAB) và (SCD) cắt nhau theo giao tuyến là đường thẳng $△$ đi qua S, song song với AB và CD.

Gọi H; K lần lượt là trung điểm của AB và CD => HK đi qua O và $HK\perp AB$.

Ta có: $\left\{\begin{array}{l}SO\perp AB\\ HK\perp AB\end{array}\right.\Rightarrow AB\perp \left(SHK\right)\Rightarrow \Delta \perp \left(SHK\right)$ (Do $\Delta //AB$).

$\Rightarrow \widehat{\left(\left(SAB\right);\left(SCD\right)\right)}=\widehat{\left(SH;SK\right)}=60°\Rightarrow SH\perp SK\Rightarrow$Tam giác SHK là tam giác đều.

Kẻ KP vuông góc SH tại P.

Do $CD//AB\subset \left(SAB\right)\Rightarrow CD//\left(SAB\right)$ nên $d\left(CD;AB\right)=d\left(CD;\left(SAB\right)\right)=d\left(K;\left(SAB\right)\right)=a$

Khi đó ta có: $\left\{\begin{array}{l}KP\perp SH\\ KP\perp AB\end{array}\right.\Rightarrow KP\perp \left(SAB\right)\Rightarrow d\left(K;\left(SAB\right)\right)=KP=a\Rightarrow SO=a$ và $HK=\frac{2a}{\sqrt{3}}$(Do tam giác SHK là tam giác đều)

Suy ra $S_{ABCD}=H{K}^2=\frac{4a^2}{3}$.

Vậy thể tích khối chóp S.ABCD là: $V_{S.ABCD}=\frac{1}{3}SO.S_{ABCD}=\frac{1}{3}a.\frac{4a^2}{3}=\frac{4}{9}{a}^3$