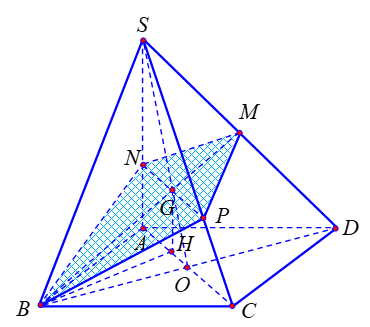
Cho hình chóp SABCD với đáy là hình chữ nhật có AB=a, BC= a căn 2, SA vuông góc ( ABCD) và SA = a căn 3 . Gọi M là trung điểm SD và (P) 

A. $\frac{2a\sqrt{2}}{3}$

B. $\frac{a\sqrt{2}}{9}$

C. $\frac{a\sqrt{2}}{3}$

D. $\frac{4a\sqrt{2}}{9}$

Trả lời

Chọn A

Dễ thấy:

$BD=AC=a\sqrt{3}$; $SB=2a$; $SD=a\sqrt{5}$ $\Rightarrow B{M}^2=\frac{2\left(B{D}^2+S{B}^2\right)-S{D}^2}{4}=\frac{9a^2}{4}$

$V_{S.ABCD}=\frac{1}{3}.S_{ABCD}.SA=\frac{a^3\sqrt{6}}{3}$

Kẻ $BH\perp AC$ thì $BH.AC=BA.BC$ $\Rightarrow BH=\frac{BA.BC}{AC}=\frac{a\sqrt{2}}{\sqrt{3}}$ $\Rightarrow \frac{AH}{AO}=\frac{2}{3}$

$\Rightarrow H$ là trọng tâm tam giác ABD

Gọi G là trọng tâm tam giác SBD  thì $GH\text{\hspace{0.17em}//\hspace{0.17em}}SA$ và $NP\text{\hspace{0.17em}//\hspace{0.17em}}AC$ vì $BM\perp NP$

Ta có:

$\frac{SG}{SO}=\frac{2}{3}$ và $\frac{SN}{SA}=\frac{SP}{SC}=\frac{2}{3}$; $NP=\frac{2}{3}AC=\frac{2a\sqrt{3}}{3}$.

Ü $\frac{V_{S.BNP}}{V_{S.BAC}}=\frac{4}{9}$ và $\frac{V_{S.MNP}}{V_{S.DAC}}=\frac{2}{9}$.

$\Rightarrow V_{S.BNMP}=\frac{1}{3}{V}_{S.ABCD}$.

Mặt khác:  $V_{S.BNMP}=\frac{1}{3}{S}_{BNMP}.d\left(S,\left(P\right)\right)\Rightarrow d\left(S,\left(P\right)\right)=\frac{3V_{S.BNMP}}{S_{BNMP}}$.

Mà $S_{BNMP}=\frac{1}{2}BM.NP\Rightarrow S_{BNMP}=\frac{a^2\sqrt{3}}{2}\Rightarrow d\left(S,\left(P\right)\right)=\frac{3V_{S.BNMP}}{S_{BNMP}}\frac{2a\sqrt{2}}{3}$   .