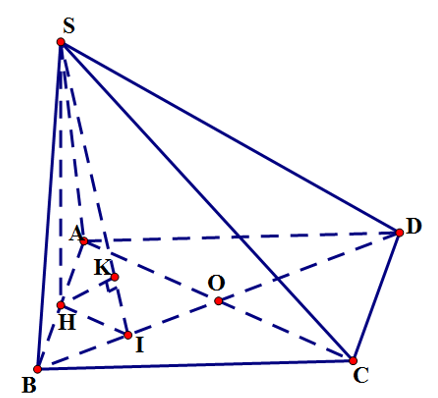
Cho hình chóp SABCD có đáy là hình vuông cạnh $a,SD=\frac{a\sqrt{17}}{2},$ hình chiếu vuông góc H của S lên mặt phẳng $\left(ABCD\right)$ là trung điểm đoạn AB Tính chiều cao của khối chóp HSBD theo a

Chọn C

Gọi O là giao điểm của AC,BD và I là trung điểm của BO

Ta có: $OI//AC\Rightarrow OI\perp BD.$

$SH\perp \left(ABCD\right)\Rightarrow SH\perp BD.$

Do đó, $BD\perp \left(SHI\right)\Rightarrow \left(SBD\right)\perp \left(SHI\right);\left(SBD\right)\cap \left(SHI\right)=SI.$

Trong $\left(SHI\right),$ dựng $HK\perp SI\Rightarrow HK\perp \left(SBD\right).$

Lúc đó, chiều cao của khối chóp $H.SBD$ là $HK.$

Xét $\Delta AHD$ vuông tại $H:HD=\sqrt{A{H}^2+A{D}^2}=\sqrt{{\left(\frac{a}{2}\right)}^2+a^2}=\frac{a\sqrt{5}}{2}.$

Xét $\Delta SHD$ vuông tại $H:HD=\sqrt{A{H}^2+A{D}^2}=\sqrt{{\left(\frac{a}{2}\right)}^2+a^2}=\frac{a\sqrt{5}}{2}.$

AC là đường chéo hình vuông cạnh $H:SH=\sqrt{S{D}^2-H{D}^2}=\sqrt{{\left(\frac{a\sqrt{17}}{2}\right)}^2-{\left(\frac{a\sqrt{5}}{2}\right)}^2}=a\sqrt{3}.$

Xét $\Delta HSI$ vuông tại H có đường cao $HK:\frac{1}{H{K}^2}=\frac{1}{S{H}^2}+\frac{1}{H{I}^2}=\frac{1}{{\left(a\sqrt{3}\right)}^2}+\frac{1}{{\left(\frac{a\sqrt{2}}{4}\right)}^2}=\frac{25}{3a^2}\Rightarrow H{K}^2=\frac{3a^2}{25}\Rightarrow HK=\frac{\sqrt{3}a}{5}.$

Vậy chiều cao của khối chóp $H.SBD$là $\frac{\sqrt{3}a}{5}.$