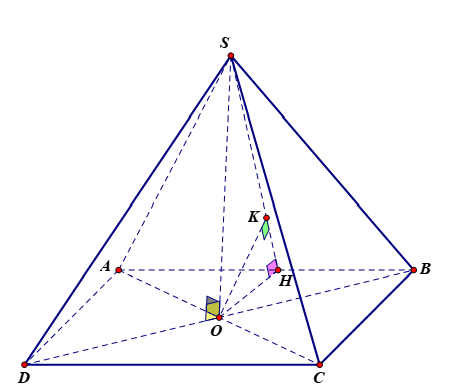
Cho hình chóp SABCD có đáy là hình thoi tâm O, AC= 2acăn 3 , BD= 2a. Hai mặt phẳng (SAC) và ( SBD) cùng vuông góc với mặt đáy ( ABCD)  .

A. $V=\frac{a^3\sqrt{3}}{9}$

B. $V=a^3\sqrt{3}$

C. $V=\frac{a^3\sqrt{3}}{3}$

D. $V=\frac{a^3\sqrt{3}}{6}$

Trả lời

Chọn C

Vì  $\left\{\begin{array}{l}\left(SAC\right)\cap \left(ABCD\right)\\ \left(SBD\right)\cap \left(ABCD\right)\\ \left(SAC\right)\cap \left(SBD\right)=SO\end{array}\right.$nên $SO\perp \left(ABCD\right)$  .

Kẻ $OH\perp AB\left(H\in AB\right)$ , $OK\perp SH\left(K\in SH\right)$  .

Mà $\left.\begin{array}{c}AB\perp OH\\ AB\perp SO\end{array}\right\}\Rightarrow AB\perp \left(SOH\right)\Rightarrow AB\perp OK$  .

Do $OK\perp SH$  nên .

$OK\perp \left(SAB\right)\Rightarrow d\left(O,\left(SAB\right)\right)=OK=\frac{a\sqrt{3}}{4}$

Xét $\Delta OAB$  vuông tại O, vì $OH\perp AB$  nên

$\frac{1}{O{H}^2}=\frac{1}{O{A}^2}+\frac{1}{O{B}^2}=\frac{4}{3a^2}\Rightarrow OH=\frac{a\sqrt{3}}{2}$.

Xét $\Delta SOH$  vuông tại O, vì $OK\perp SH$  nên

$\frac{1}{O{K}^2}=\frac{1}{O{S}^2}+\frac{1}{O{H}^2}\iff \frac{16}{3a^2}=\frac{1}{O{S}^2}+\frac{4}{3a^2}\Rightarrow SO=\frac{1}{2}a$

Diện tích mặt đáy ABCD  là $S.ABCD=\frac{1}{2}\cdot AC\cdot BD=2a^2\sqrt{3}$ .

Thể tích hình chóp SABCD  là  $V_{S.ABCD}=\frac{1}{3}\cdot S_{ABCD}\cdot SO=\frac{a^3\sqrt{3}}{3}$ .