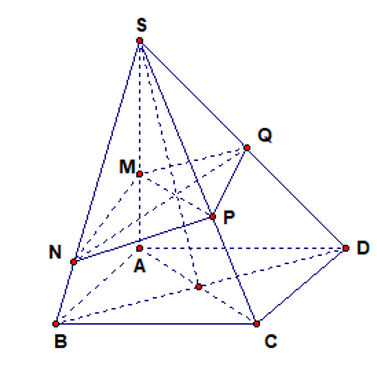
Cho hình chóp SABCD có đáy là hình bình hành và có thể tích V  . Trên cạnh SA  ,  SB lần lượt lấy các điểm M,N  sao cho

A. $\frac{15}{28}V$

B. $\frac{5}{9}V$

C. $\frac{15}{22}V$

D. $\frac{4}{9}V$

Trả lời

Chọn A

Đặt $x=\frac{SP}{SC}\left(0\le x\le 1\right)$

Vì hình chóp $S.ABCD$ có đáy là hình bình hành nên ta có $\frac{SA}{SM}+\frac{SC}{SP}=\frac{SB}{SN}+\frac{SD}{SQ}(*)$

Áp dụng vào bài: $\frac{3}{2}+\frac{1}{x}=\frac{4}{3}+\frac{SD}{SQ}$$\iff \frac{SD}{SQ}=\frac{x+6}{6x}$ .

Mặt khác $\frac{V_{S.MNP}}{V_{S.ABC}}=\frac{SM}{SA}\frac{SN}{SB}\frac{SP}{SC}\Rightarrow \frac{V_{S.MNP}}{V_{S.ABCD}}=\frac{1}{2}.\frac{SM}{SA}.\frac{SN}{SB}.\frac{SP}{SC}\left(1\right)$

$\left(1\right)+\left(2\right)$ vế theo vế suy ra $\frac{V_{S.MNPQ}}{V_{S.ABCD}}=\frac{1}{2}.\left(\frac{SM}{SA}.\frac{SN}{SB}.\frac{SP}{SC}+\frac{SM}{SA}.\frac{SQ}{SD}.\frac{SP}{SC}\right)$

$\Rightarrow V_{S.MNPQ}=\frac{V}{2}.\left(\frac{2}{3}.\frac{3}{4}.x+\frac{2}{3}.\frac{6x}{6+x}.x\right)=\frac{V}{2}.\left(\frac{x}{2}+\frac{4x^2}{x+6}\right)$

Xét hàm số $f\left(x\right)=\frac{x}{2}+\frac{4x^2}{x+6}$  trên đoạn $\left[0;1\right]$

$f^{\text{'}}\left(x\right)>0,\forall x\in \left[0;1\right]$ nên hàm số đồng biến trên $\left[0;1\right]$ , suy ra $\underset{\left[0;1\right]}{Max}f=f\left(1\right)=\frac{15}{14}$

Vậy $Max{V}_{S.MNPQ}=\frac{15}{28}V$  nên chọnA.