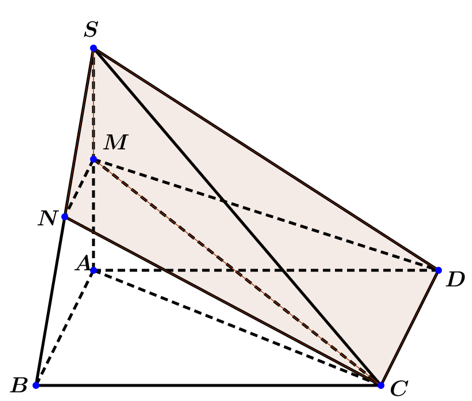
Cho hình chóp SABCD có đáy hình vuông, cạnh bên SA vuông góc với đáy. Gọi M,N là trung điểm của SA, SB
42
04/05/2024
Cho hình chóp SABCD có đáy hình vuông, cạnh bên SA vuông góc với đáy. Gọi M,N là trung điểm của . Mặt phẳng chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần và là
A. 1
B.
C.
D.
Trả lời
Chọn C
Xét hình chóp có đáy hình vuông, cạnh bên SA vuông góc với đáy với M,N là trung điểm của ta có
Mà trong SABCD ta có .
Suy ra
Trong SACD ta có
Suy ra
Vậy
Suy ra
.