Cho hình chóp SABCD có đáy ABC là tam giác đều, SA vuông góc với mặt phẳng ( ABC). Góc giữa hai mặt phẳng
79
29/04/2024
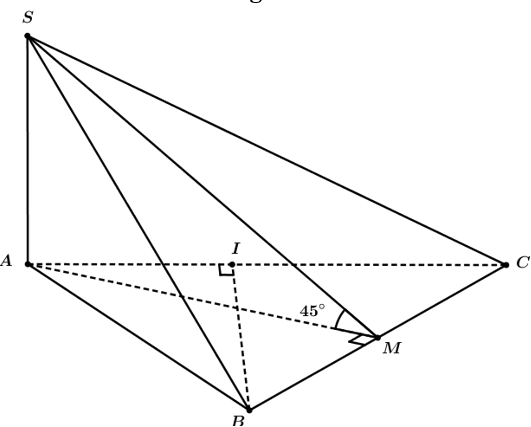
Cho hình chóp SABCD có đáy ABC là tam giác đều, SA vuông góc với mặt phẳng ( ABC). Góc giữa hai mặt phẳng (SBC) và mặt phẳng (ABC) bằng 45, . Tính khoảng cách từ điểm B đến mặt phẳng .
Trả lời
Gọi M là trung điểm BC Vì tam giác ABC đều nên (1).
Mặt khác, tam giác SBC cân tại S nên (2).
Từ (1) và (2) ta có góc giữa hai mặt phẳng và là .
Xét tam giác SAM vuông tại A có góc . Từ đó suy ra tam giác SAM vuông cân tại A
và
Gọi I là trung điểm của BC . Vì tam giác ABC đều nên
Ta có:
Vậy