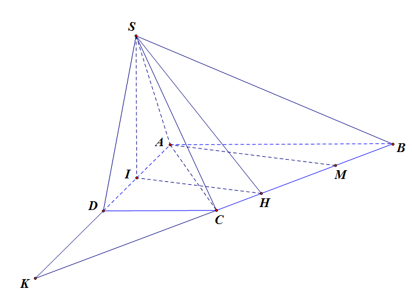
Cho hình chóp SABCDcó đáy ABCDlà hình thang vuông tại $A,D;AB=AD=2a;CD=a.$Góc giữa hai mặt phẳng ( SBC)và ( ABCD)là 60$°$Gọi Ilà trung điểm của AD biết hai mặt phẳng ( SBI), ( CBI) cùng vuông góc với mặt phẳng ( ABCD)Tính thể tích khối chóp SABCD

Chọn A

Ta có:

$\left(SBI\right)\cap \left(SCI\right)=SI\Rightarrow SI\perp \left(ABCD\right).$

Kẻ $IH\perp BC\left(H\in BC\right)$ ,$SI\perp \left(ABCD\right)\Rightarrow SI\perp BC$

Suy ra: $\left(\left(SBC\right),\left(ABCD\right)\right)=\widehat{SHI}={60}^o$ .

Kẻ $AM\perp BC.$

Trong $\left(ABCD\right),BC\cap AD=K\Rightarrow D$  là trung điểm AK

Ta có: $S_{ABC}=\frac{1}{2}.2a.2a=2a^2=\frac{1}{2}AM.BC\Rightarrow AM=\frac{4a^2}{BC}=\frac{4a\sqrt{5}}{5}.$

Áp dụng định lý Thales trong $\Delta KAM:\frac{KI}{KA}=\frac{IH}{AM}\Rightarrow \frac{IH}{AM}=\frac{3}{4}\Rightarrow IH=\frac{3a\sqrt{5}}{5}.V$

Suy ra: $SI=IH.\tan {60}^o=\frac{3a\sqrt{15}}{5}.$

$V=\frac{1}{3}.SI.S_{ABCD}=\frac{1}{3}.\frac{3a\sqrt{15}}{5}.\frac{\left(a+2a\right).2a}{2}=\frac{3a^3\sqrt{15}}{5}.$