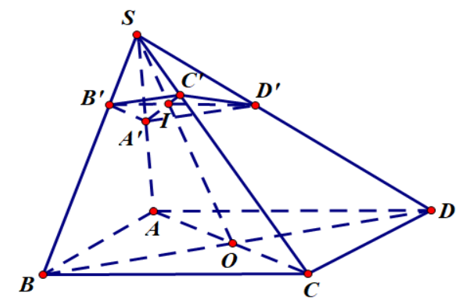
Cho hình chóp SABCD có đáy ABCD là hình bình hành. Trên các cạnh SA, SB,SC  lần lượt lấy các điểm A', B', C' sao cho $SA=2S{A}^{\text{'}},SB=3S{B}^{\text{'}},SC=4S{C}^{\text{'}}$, mặt phẳng $\left(A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}\right)$ cắt cạnh SD tại D'. Gọi $V_1,V_2$ lần lượt là thể tích hai khối chóp $S.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ và $S.ABCD$. Tỉ số $\frac{V_1}{V_2}$bằng

Chọn D

Gọi $O=AC\cap BD;I=A^{\text{'}}{C}^{\text{'}}\cap SO$. Gọi $D^{\text{'}}=B^{\text{'}}I\cap SD$. Khi đó $D^{\text{'}}$ là giao điểm của SD và $\left(A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}\right)$.

Ta có $\frac{SA}{S{A}^{\text{'}}}+\frac{SC}{S{C}^{\text{'}}}=2\frac{SO}{SI}\Rightarrow \frac{SO}{SI}=3$.

Ta lại có $\frac{SB}{S{B}^{\text{'}}}+\frac{SD}{S{D}^{\text{'}}}=2\frac{SO}{SI}\Rightarrow \frac{SD}{S{D}^{\text{'}}}=3$.

Ta có $V_1=V_{S.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}+V_{S.A^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}$.

Mà $\frac{V_{S.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}}{V_{S.ABC}}=\frac{S{A}^{\text{'}}}{SA}.\frac{S{B}^{\text{'}}}{SB}.\frac{S{C}^{\text{'}}}{SC}=\frac{1}{24}\Rightarrow V_{S.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}=\frac{1}{48}{V}_2$.

$\frac{V_{S.A^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}}{V_{S.ACD}}=\frac{S{A}^{\text{'}}}{SA}.\frac{S{C}^{\text{'}}}{SC}.\frac{S{D}^{\text{'}}}{SD}=\frac{1}{24}\Rightarrow V_{S.A^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}=\frac{1}{48}{V}_2$.

Vậy ta được $V_1=V_{S.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}+V_{S.A^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}=\frac{1}{24}{V}_2\Rightarrow \frac{V_1}{V_2}=\frac{1}{24}$.