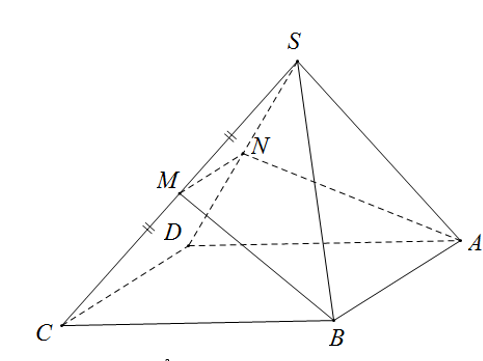
Cho hình chóp SABCD có đáy ABCD là hình bình hành. Mặt phẳng ( anpha) đi qua A, B và trung điểm M của SC Mặt phẳng( anpha) chia khối
36
30/04/2024
Cho hình chóp SABCD có đáy ABCD là hình bình hành. Mặt phẳng đi qua A, B và trung điểm M của SC Mặt phẳng chia khối chóp đã cho thành hai phần có thể tích lần lượt là với Tính tỉ số
A.
B.
C.
D.
Trả lời
Chọn D
Từ M kẻ Lúc đó, mặt phẳng
Ta có:
Suy ra:
Mà
Suy ra:
Vậy