Cho hình chóp S.ABCD có đáy là hình thang với AB song song với CD, CD = 7 AB. Gọi M trên cạnh SA sao cho SM/SA = k
24
30/11/2024
Cho hình chóp S.ABCD có đáy là hình thang với AB song song với CD, CD = 7 AB. Gọi M trên cạnh SA sao cho SMSA=k, (0<k<1). Tìm giá trị của k để (CDM) chia khối chóp thành hai phần có thể tích bằng nhau.
A. k=−7+√532
B. k=−7+√652
C. k=−7+√714
D. k=−7+√532
Trả lời
Đáp án đúng là: B
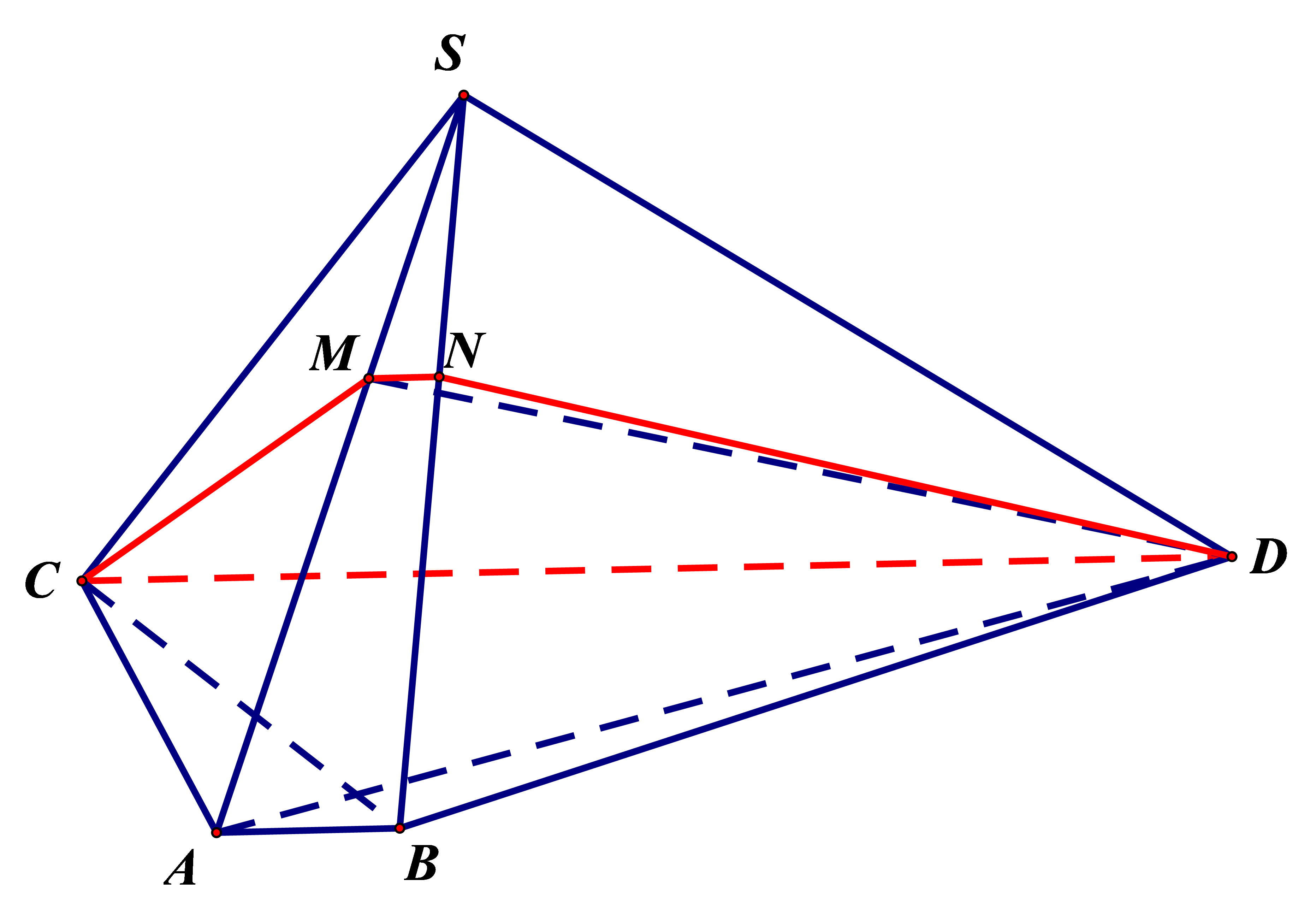
Ta có: (CMD)∩(SAB)=Δ{qua M// CD
Gọi N=Δ∩SB⇒N=(CDM)∩SB. Khi đó, ta có: SMSA=SNSB=k
Đồng thời (CDM) chia khối chóp thành hai phần: S.CMND và ABCDMN.
Ta có: VS.CDMN=VS.DMC+VS.MNC.
Lại có: VS.DMCVS.DAC=SMSA=k, VS.MNCVS.ABC=SMSA.SNSB=k2
Suy ra VS.CDMN=VS.DMC+VS.MNC=kVS.DAC+k2VS.ABC.
Mà CD=7AB⇒SACD=7.SABC⇒VS.ACD=7VS.ABC.
Do đó, ta có:
VS.CDMN=7kVS.ABC+k2VS.ABC=(k2+7k)VS.ABC=18(k2+7k)VS.ABCD.
Lại có VS.CDMN=12VS.ABCD (do (CDM) chia thành hai phần có thể tích bằng nhau)
Suy ra 18(k2+7k)VS.ABCD=12VS.ABCD⇔k2+7k=4⇔k=−7+√652.

