Cho hàm số y = f(x) có đạo hàm liên tục trên $ℝ$ và f(0) = 0. Đồ thị hàm số y = f’(x) như hình vẽ bên dưới.

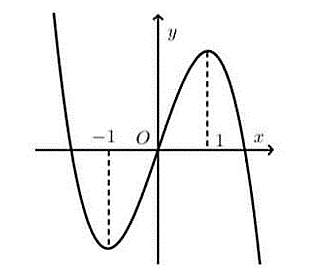
Có bao nhiêu số nguyên dương a để hàm số $y=\left|2f\left(\sin x\right)-3\cos 2x-a+9\right|$ đồng biến trên khoảng $\left(0;\frac{\pi }{2}\right)$?

Đáp án đúng là: D

Ta có: $y=\left|2f\left(\sin x\right)-3\left(1-2{\sin }^{2}x\right)-a+9\right|$$=\left|2f\left(\sin x\right)+6{\sin }^{2}x+6-a\right|$

Đặt $t=\sin x,t\in \left(0;1\right)$.

Khi đó, ta có: $y=\left|2f\left(t\right)+6t^2+6-a\right|=\sqrt{{\left[2f\left(t\right)+6t^2+6-a\right]}^2}$

Ta có: $y^{\text{'}}=\frac{\left(2f\left(t\right)+6t^2+6-a\right)\left(2f\text{'}\left(t\right)+12t\right)}{\sqrt{{\left[2f\left(t\right)+6t^2+6-a\right]}^2}}$.

Để hàm số đồng biến trên (0;1) thì

$y^{\text{'}}>\mathrm{0,}\forall t\in \left(0;1\right)\iff \left(2f\left(t\right)+6t^2+6-a\right)\left(2f^{\text{'}}\left(t\right)+12t\right)>\mathrm{0,}\forall t\in \left(0;1\right)$.(1)

Dựa vào đồ thị f'(t) ta thấy $2f^{\text{'}}\left(t\right)+12t>\mathrm{0,}\forall t\in \left(0;1\right)$.

Do đó, $\left(1\right)\iff 2f\left(t\right)+6t^2+6-a>\mathrm{0,}\forall t\in \left(0;1\right)$

$\iff a<2f\left(t\right)+6t^2+\mathrm{6,}\forall t\in \left(0;1\right)$$\Rightarrow a\le \underset{\left[0;1\right]}{\min }\left\{2f\left(t\right)+6t^2+6\right\}$.

Xét hàm số $g\left(t\right)=2f\left(t\right)+6t^2+6$ trên [0;1].

Ta có: $g^{\text{'}}\left(t\right)=2f^{\text{'}}\left(t\right)+12t>\mathrm{0,}\forall t\in \left(0;1\right)$ suy ra hàm số g(t) đồng biến trên (0;1)

Do đó, $\underset{\left[0;1\right]}{\min }g\left(t\right)=g\left(0\right)=2f\left(0\right)+{6.0}^2+6=6$.

Vậy $a\le 6$. Mà $a\in {\mathbb{N}}^{*}$ suy ra $a\in \left\{\mathrm{1,2,3,4,5,6}\right\}$.