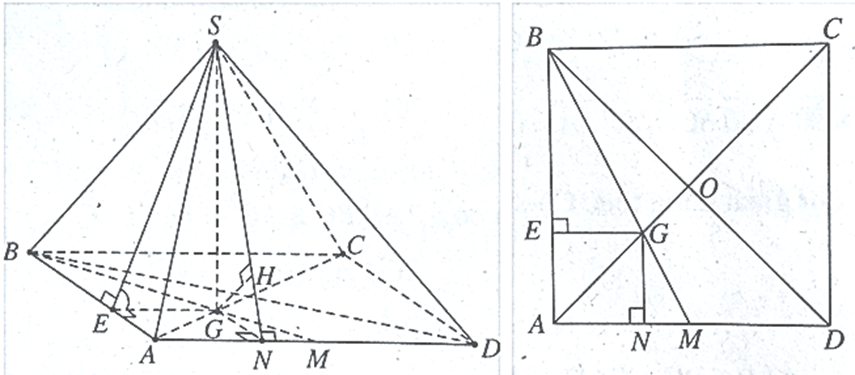
+ Xác định góc của (SAB) và mặt phẳng đáy.

Gọi G là trọng tâm tam giác ABD và E là hình chiếu của G lên AB. Ta có:

AB ^ SG và AB ^ GEÞ AB ^ (SEG) Þ AB ^ SE.

SE ^ AB và GE ^AB\(\left( {\widehat {\left( {SAB} \right)\,,\,\left( {ABCD} \right)}} \right) = \widehat {SEG} = 60^\circ \)

+ Xác định khoảng cách từ B đến mặt phẳng (SAD).

Hạ GN ^ AD. Tương tự như trên, ta có: AD ^ GN và AD ^ SGÞ AD ^ (SGN)

Hạ GH ^ SN, ta có GH ^ (SAD) suy ra khoảng cách từ G đến (SAD) là GH.

+ Tính GH.

Trong tam giác vuông SGN, ta có: \(\frac{1}{{G{H^2}}} = \frac{1}{{G{S^2}}} + \frac{1}{{G{N^2}}}\) (1)

Do GN // AB nên \(\frac{{GN}}{{BA}} = \frac{{MG}}{{MB}} = \frac{1}{3}\)

Ta có: \[GN = \frac{{BA}}{3} = \frac{a}{3}\]

Trong tam giác SGE, ta được \(GS = GE\,.\,\tan 60^\circ = \frac{{a\sqrt 3 }}{3}\) (Do GE = GN)

Thế vào (1) ta được:

\(\frac{1}{{G{H^2}}} = \frac{1}{{G{S^2}}} + \frac{1}{{G{N^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{a}{3}} \right)}^2}}} = \frac{{36}}{{3{a^2}}}\)

\( \Rightarrow GH = \frac{{a\sqrt 3 }}{6}\)

Ta có: M Î(SAD) và  MB= 3MG

\( \Rightarrow d\left( {B,\;\left( {SAD} \right)} \right) = 3d\left( {G,\;\left( {SAD} \right)} \right) = 3\,.\,\frac{{a\sqrt 3 }}{6} = \frac{{a\sqrt 3 }}{2}\).