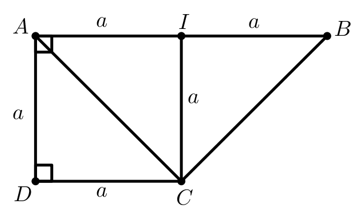
Cho hình chóp SABCD , có đáy  ABCD là hình thang vuông tại A  và D  , có AB= 2a , AD=DC=a ,  SA=a và $SA\perp \left(ABCD\right)$ .  của góc giữa hai mặt phẳng (SBC) và $\left(ABCD\right)$  là

Gọi I  là trung điểm của AB  suy ra $AI=\frac{1}{2}AB=a$ .

Suy ra  $AC\perp CB$(1).

Mà  $SA\perp \left(ABCD\right)\Rightarrow SA\perp CB$(2)

Từ (1) và (2) suy ra   $SC\perp CB$

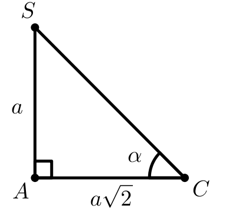
Vậy góc giữa hai mặt phẳng (SBC) và (iABCD) là góc giữa hai đường thẳng trong hai mặt phẳng cùng vuông góc với giao tuyến, tức là góc $\widehat{SCA}=\alpha$.

Do đó $\tan \alpha =\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$ .