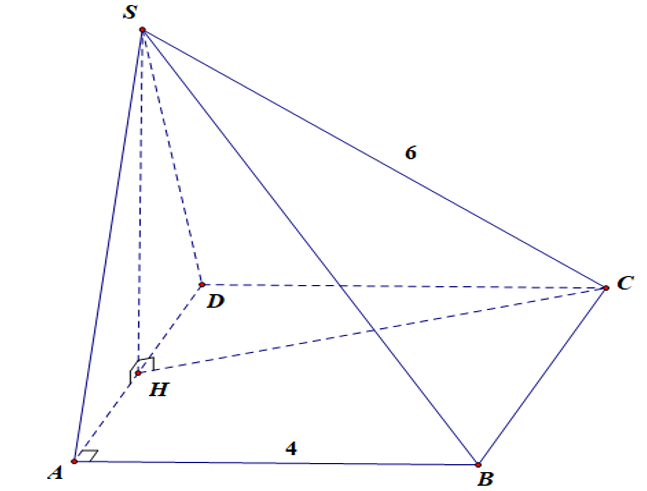
Cho hình chóp $S.ABCD$  có đáy ABCD   là hình chữ nhật với $AB=4,SC=6$  và mặt bên SAD là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích lớn nhất $V_{\max }$của khối chóp $S.ABCD$  .

Chọn A

Gọi  là trung điểm của . Theo giả thiết, suy ra $SH\perp \left(ABCD\right)$  .

Đặt $x=AD\left(x>0\right)$ . Suy ra $S_{ABCD}=4x$

$H{C}^2=16+\frac{x^2}{4}$.

$SH=\sqrt{36-16-\frac{x^2}{4}}=\sqrt{20-\frac{x^2}{4}}\text{ , }\left(0<x<4\sqrt{5}\right)$

Suy ra $V_{S.ABCD}=\frac{1}{3}.4x.\sqrt{20-\frac{x^2}{4}}=\frac{2x\sqrt{80-x^2}}{3}=\frac{2\sqrt{x^2\left(80-x^2\right)}}{3}\le \frac{80}{3}$  (Bất đẳng thức Cauchy)

$V_{S.ABCD}=V_{\text{max}}=\frac{80}{3}\iff x^2=80-x^2\iff x=2\sqrt{10}.$