Giải SGK Toán 11 (Cánh diều) Bài 3: Đường thẳng và mặt phẳng song song

Giải Toán 11 Bài 3: Đường thẳng và mặt phẳng song song

Câu hỏi khởi động trang 101 Toán 11 Tập 1: Trong thực tiễn, ta thường gặp nhiều đồ dùng, vật thể gợi nên hình ảnh đường thẳng song song với mặt phẳng. Chẳng hạn, thanh barrier song song với mặt phẳng (Hình 44).

Thế nào là đường thẳng song song với mặt phẳng trong không gian?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Đường thẳng song song với mặt phẳng trong không gian là đường thẳng song song với một đường thẳng khác nằm trong mặt phẳng đó.

I. Đường thẳng song song với mặt phẳng

Hoạt động 1 trang 101 Toán 11 Tập 1: a) Trong Hình 44, thanh barrier và mặt phẳng gợi nên hình ảnh đường thẳng d và mặt phẳng (P). Cho biết đường thẳng d và mặt phẳng (P) có điểm chung hay không.

b) Cho đường thẳng d và mặt phẳng (P). Hãy cho biết các khả năng có thể xảy ra đối với số điểm chung của d và (P).

Lời giải:

a) Trong Hình 44 đường thẳng d và mặt phẳng (P) không có điểm chung.

b)

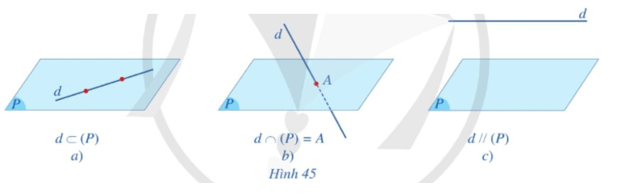
Ở Hình 45a): Đường thẳng d nằm trong mặt phẳng (P) nên có vô số điểm chung.

Ở Hình 45b): Đường thẳng d cắt mặt phẳng (P) tại một điểm nên có 1 điểm chung.

Ở Hình 45c): Đường thẳng d song song với mặt phẳng (P) nên không có điểm chung với nhau.

Luyện tập 1 trang 102 Toán 11 Tập 1: Quan sát các xà ngang trên sân tập thể dục Hình 47. Hãy cho biết ở vị trí tương đối của các xà ngang đó đối với mặt sàn.

Lời giải:

Vị trí tương đối của xà ngang với mặt sàn là đường thẳng song song với mặt phẳng.

II. Điều kiện và tính chất

Hoạt động 2 trang 102 Toán 11 Tập 1: Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng a’ nằm trong (P) (Hình 48). Gọi (Q) là mặt phẳng xác định bởi hai đường thẳng song song a, a’.

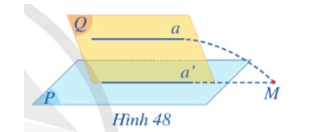
a) Giả sử a cắt (P) tại M. Đường thẳng a có cắt đường thẳng a’ tại M hay không?

b) Nêu vị trí tương đối của đường thẳng a và mặt phẳng (P). Vì sao?

Lời giải:

a) Do a’ ⊂ (P) và a’ ⊂ (Q) nên (P) ∩ (Q) = a’.

Mà a cắt (P) tại M nên M ∈ (P)

Lại có M ∈ a, a ⊂ (Q) nên M ∈ (Q)

Suy ra M là giao điểm của (P) và (Q).

Do đó giao tuyến a’ của hai mặt phẳng đi qua điểm M.

Vậy đường thẳng a cắt đường thẳng a’ tại M.

b) Theo câu a, nếu a cắt (P) tại M thì đường thẳng a và đường thẳng a’ cắt nhau tại M.

Điều này là mâu thuẫn với giả thiết là hai đường thẳng a và a’ song song.

Do đó a không có điểm chung với (P) nên a // (P).

Luyện tập 2 trang 102 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, AD. Các đường thẳng MN, NP, PM có song song với mặt phẳng (BCD) không? Vì sao?

Lời giải:

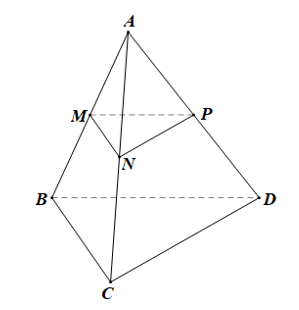
• Xét $∆$ABC có M, N lần lượt là trung điểm của AB, AC nên MN là đường trung bình của tam giác

Do đó MN // BC

Lại có BC ⊂ (BCD)

Suy ra MN // (BCD).

• Chứng minh tương tự ta cũng có NP // CD.

Mà CD ⊂ (BCD)

Suy ra NP // (BCD).

• Tương tự, MP // BD mà BD ⊂ (BCD) .

Suy ra MP // (BCD).

Hoạt động 3 trang 102, 103 Toán 11 Tập 1: Cho đường thẳng a song song với mặt phẳng (P). Cho mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b. (Hình 51).

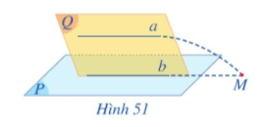
a) Giả sử a cắt b tại M. Đường thẳng a có cắt mặt phẳng (P) tại M hay không?

b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?

Lời giải:

a) Ta có a ∩ b = {M} nên M ∈ b

Mà b ⊂ (P), do đó M ∈ (P).

Lại có M ∈ a.

Vậy đường thẳng a cắt mặt phẳng (P) tại M.

b) Theo câu a, nếu a cắt b tại M thì a cắt (P) tại M, điều này mâu thuẫn với giả thiết đường thẳng a song song với mặt phẳng (P).

Do đó a và b không cắt nhau và cùng nằm trong mặt phẳng (Q).

Suy ra a // b.

Vậy hai đường thẳng a và b song song với nhau.

Luyện tập 3 trang 103 Toán 11 Tập 1: Ở Ví dụ 3, xác định giao tuyến của mặt phẳng (R) với các mặt phẳng (ABD), (BCD), (ACD).

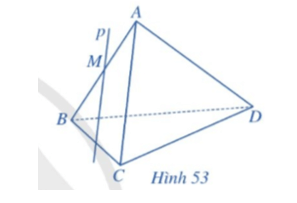
Lời giải:

• Áp dụng định lí 2, ta có:

(R) đi qua M và song song với BD, mà BD ⊂ (ABD) nên mặt phẳng (R) cắt (ABD) theo giao tuyến a đi qua M và song song với BD.

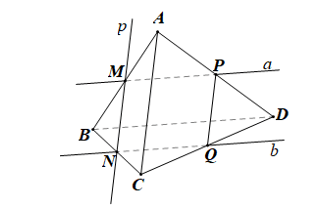
• Gọi N là giao điểm của p và BC.

Khi đó N ∈ (R).

Áp dụng định lí 2, ta có:

(R) đi qua N và song song với BD, mà BD ⊂ (BCD) nên mặt phẳng (R) cắt (BCD) theo giao tuyến b đi qua N và song song với BD.

• Gọi P là giao điểm của a và AD, Q là giao điểm của b và CD.

Khi đó P ∈ (R) và P ∈ (ACD) nên P là giao điểm của (R) và (ACD);

            Q ∈ (R) và Q ∈ (ACD) nên Q là giao điểm của (R) và (ACD).

Vậy (R) ∩ (ACD) = PQ.

Hoạt động 4 trang 103 Toán 11 Tập 1: Cho hai mặt phẳng (P), (Q) cùng song song với đường thẳng a và (P) ∩ (Q) = b (Hình 54).

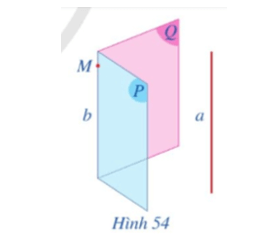
a) Lấy một điểm M trên đường thẳng b. Gọi b’, b” lần lượt là các giao tuyến của mặt phẳng (M, a) với (P) và mặt phẳng (M, a) với (Q). Cho biết b’ và b” có trùng với b hay không.

b) Nêu vị trí tương đối của hai đường thẳng a và b. Vì sao?  

Lời giải:

a) • Ta có: M ∈ b và (P) ∩ (Q) = b;

Suy ra M ∈ (P).

Mà M ∈ (M, a)

Do đó M là giao điểm của (P) và (M, a).

Lại có b’ = (P) ∩ (M, a)

Suy ra đường thẳng b’ đi qua M.

Tương tự ta cũng chứng minh được b’’ đi qua điểm M.

• Ta có: a // (P);

             a ⊂ (M, a)

             (M, a) ∩ (P) = b’

Do đó a // b’.

Tương tự ta cũng có a // b’’.

Do đó b’ // b’’.

Mặt khác: (P) ∩ (Q) = b;

                 (M, a) ∩ (P) = b’;

                 (M, a) ∩ (Q) = b’’;

                 b // b’’.

Do đó b // b’ // b’’.

Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau.

b) Vì a // b’ nên a // b (do b ≡ b’).

Luyện tập 4 trang 104 Toán 11 Tập 1: Trong Hình 56, hai mặt tường của căn phòng gợi nên hình ảnh hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến b, mép cột gợi nên hình ảnh đường thẳng a. Cho biết đường thẳng a có song song với giao tuyến b hay không.

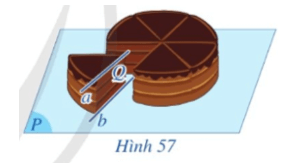
Lời giải:

Ta có: a // (P);

           a // (Q);

           (P) ∩ (Q) = b.

Do đó theo hệ quả định lí 2 ta có a // b.

Bài tập

Bài 1 trang 104 Toán 11 Tập 1: Trong phòng họp của lớp, hãy nêu những hình ảnh về đường thẳng song song với mặt phẳng.

Lời giải:

Gợi ý những hình ảnh về đường thẳng song song với mặt phẳng: đường chân tường và trần nhà; mép cột tường và bức tường; …

Bài 2 trang 104 Toán 11 Tập 1: Trong Hình 57, khi cắt bánh sinh nhật, mặt cắt và mặt khay đựng bánh lần lượt gợi nên hình ảnh mặt phẳng (Q) và mặt phẳng (P); mép trên và mép dưới của lát cắt lần lượt gợi nên hình ảnh hai đường thẳng a và b trong đó a song song với mặt phẳng (P). Cho biết hai đường thẳng a, b có song song với nhau hay không.

Lời giải:

Ta có: a // (P);

           a ⊂ (Q);

           (P) ∩ (Q) = b.    

Do đó theo định lí 2, a // b.

Vậy hai đường thẳng a, b song song với nhau.

Bài 3 trang 104 Toán 11 Tập 1: Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABD, điểm I nằm trên cạnh BC sao cho BI = 2IC. Chứng minh rằng IG song song với mặt phẳng (ACD).

Lời giải:

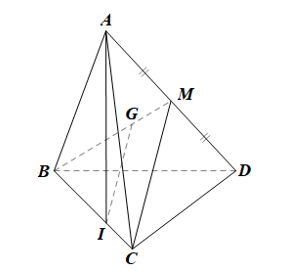
Gọi M là trung điểm của AD.

• Xét $∆$ABD có G là trọng tâm tam giác nên $\frac{BG}{GM}=\frac{2}{1}$ .

Theo bài, BI = 2IC nên $\frac{BI}{IC}=\frac{2}{1}$

• Trong mặt phẳng (BCM):

Xét $∆$BCM có: $\frac{BI}{IC}=\frac{BG}{GM}=\frac{2}{1}$ , suy ra IG // CM (định lí Thalès đảo)

• Ta có: IG // CM; CM ⊂ (ACD)

Do đó IG // (ACD).

Bài 4 trang 104 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AB và CD. Chứng minh rằng đường thẳng MN song song với giao tuyến d của hai mặt phẳng (SBC) và (SAD).

Lời giải:

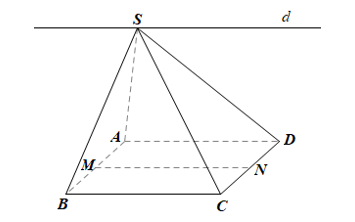
• Ta có: S ∈ (SAD) và S ∈ (SBC) nên S là giao điểm của (SAD) và (SBC).

Lại có: AD // BC (do ABCD là hình bình hành);

            AD ⊂ (SAD);

            BC ⊂ (SBC).

Do đó giao tuyến d của hai mặt phẳng (SAD) và (SBC) là đường thẳng đi qua S và song song với AD, BC.

• Vì M, N lần lượt là trung điểm của AB và CD nên MN là đường trung bình

Do đó MN // BC // AD.

Ta có: MN // BC mà BC ⊂ (SBC) nên MN // (SBC);

           MN // AD mà AD ⊂ (SAD) nên MN // (SAD).

Có: MN // (SBC);

       MN // (SAD);

       (SAD) ∩ (SBC) = d

Suy ra MN // d.

Bài 5 trang 104 Toán 11 Tập 1: Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).

Lời giải:

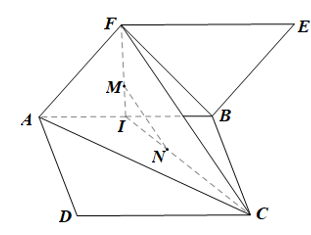
Gọi I là trung điểm của AB.

Xét DABF có M là trọng tâm của tam giác nên $\frac{FM}{MI}=\frac{2}{1}$ ;

Xét DABC có N là trọng tâm của tam giác nên $\frac{NC}{NI}=\frac{2}{1}$ ;

Trong mặt phẳng ACF, xét $∆$ACF có $\frac{FM}{MI}=\frac{NC}{NI}=\frac{2}{1}$

Suy ra MN // FC (theo định lí Thalès)

Mà FC ⊂ (ACF).

Do đó MN // (ACF).

Bài 6 trang 104 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Lấy điểm M trên cạnh AD sao cho AD = 3AM. Gọi G, N lần lượt là trọng tâm của tam giác SAB, ABC.

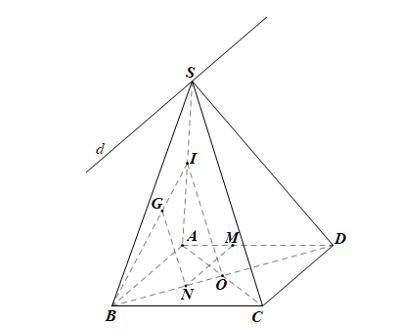
a) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).

b) Chứng minh rằng MN song song với mặt phẳng (SCD) và NG song song với mặt phẳng (SAC).

Lời giải:

a) Ta có: S ∈ (SAB) và S ∈ (SCD) nên S là giao điểm của (SAB) và (SCD).

Lại có: AB // CD (do ABCD là hình bình hành);

            AB ⊂ (SAB);

            CD ⊂ (SCD).

Do đó giao tuyến của hai mặt phẳng (SAB) và (SCD) là đường thẳng d đi qua S và song song với AB, CD.

b) • Gọi O là tâm của hình bình hành, khi đó BO = OD = $\frac{1}{2}$ BD.

Xét DABC có N là trọng tâm của tam giác nên $\frac{BN}{BO}=\frac{2}{3}$  do đó $\frac{BN}{BD}=\frac{BN}{2BO}=\frac{1}{2}.\frac{2}{3}=\frac{1}{3}$ .

Theo bài, AD = 3AM nên $\frac{AM}{AD}=\frac{1}{3}$

Trong mặt phẳng (ABCD), xét $∆$ABD có  $\frac{AM}{AD}=\frac{BN}{BD}=\frac{1}{3}$

Do đó MN // AB (theo định lí Thalès đảo)

Trong mặt phẳng (ABCD) có: AB // CD và MN // AB nên MN // CD.

Lại có CD ⊂ (SCD)

Do đó MN // (SCD).

• Gọi I là trung điểm của SA.

Xét $∆$SAB có G là trọng tâm của tam giác nên $\frac{BG}{BI}=\frac{2}{3}$

Trong (BIO), xét DBIO có: $\frac{BG}{BI}=\frac{BN}{BO}=\frac{2}{3}$

Suy ra GN // IO (theo định lí Thalès đảo)

Mà IO ⊂ (SAC) nên GN // (SAC).

Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:

Bài 1: Đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song trong không gian

Bài 4: Hai mặt phẳng song song

Bài 5: Hình lăng trụ và hình hộp

Bài 6: Phép chiếu song song. Hình biểu diễn của một hình không gian