Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a; SA vuông góc với mặt phẳng ( ABC); góc giữa đường thẳng
42
29/04/2024
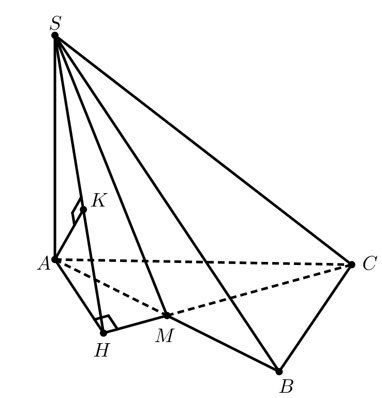
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a; SA vuông góc với mặt phẳng ( ABC); góc giữa đường thẳng SB và mặt phẳng ( ABC) bằng 60. Gọi M là trung điểm của cạnh AB. Tính khoảng cách từ B đến mặt phẳng ( SMC).
A.
B. a
C.
D.
Trả lời
Chọn C
Vì M là trung điểm của AB nên .
Trong ( ABC) , kẻ tại H.
Ta có
Hay theo giao tuyến SH.
Kẻ .
đều trung tuyến CM đồng thời là tia phân giác
.
Vì .
Ta có .