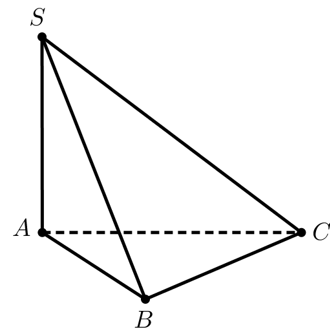
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh 2a  , hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy. Góc giữa cạnh bên SB và mặt phẳng (ABC) là $60°$ . Tính thể tích V  khối chóp SABC  .

Chọn D

Do hai mặt bên  ( SAB) và ( SAC)  cùng vuông góc với đáy nên suy ra $SA\perp \left(ABC\right)$ .

$\widehat{\left(SB,\left(ABC\right)\right)}=\widehat{SBA}={60}^{\text{o}}$.

Trong tam giác vuông SAB  , ta có $SA=AB.\tan \widehat{SBA}=2\sqrt{3}a$    .