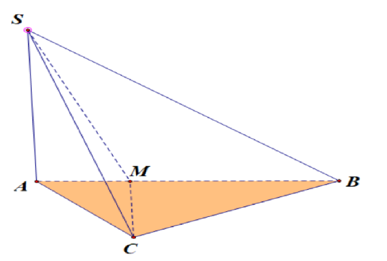
Cho hình chóp SABC có AC= a, BC=2a, $\widehat{ACB}={120}^0$. Cạnh bên SA vuông góc ( ABC), đường thẳng SC tạo với mặt phẳng ( SAB) một góc bằng 30$°$. Tính thể tích khối chóp SABC.

Chọn C

Kẻ CM vuông góc với AB. Khi dó góc tạo bởi SC và ( SAB) chính là góc $\widehat{MSC}=30°$. $S_{ABC}=\frac{1}{2}CA.CB.\sin {120}^0=\frac{a^2\sqrt{3}}{2}$

$A{B}^2=a^2+{\left(2a\right)}^2-2.a.2a.c{\text{os120}}^0=7a^2\Rightarrow AB=a\sqrt{7}$

$S_{ABC}=\frac{1}{2}AB.CM\Rightarrow CM=\frac{2S_{ABC}}{AB}=\frac{2.\frac{a^2\sqrt{3}}{2}}{a\sqrt{7}}=\frac{a\sqrt{3}}{\sqrt{7}}$

Trong tam giác SMC vuông tại M có $SM=\frac{MC}{\tan {30}^0}=\frac{a\sqrt{3}/\sqrt{7}}{\sqrt{3}/3}=\frac{3a}{\sqrt{7}}$

Trong tam giác AMC  vuông tại M có $AM=\sqrt{A{C}^2-C{M}^2}=\sqrt{a^2-\frac{3a^2}{7}}=\frac{2a}{\sqrt{7}}$

Trong tam giác SAM vuông tại A có $SA=\sqrt{S{M}^2-A{M}^2}=\sqrt{\frac{9a^2}{7}-\frac{4a^2}{7}}=\frac{a\sqrt{5}}{\sqrt{7}}$

Vậy $V_{SABC}=\frac{1}{3}.S_{ABC}.SA=\frac{1}{3}\frac{a^2\sqrt{3}}{2}.\frac{a\sqrt{5}}{\sqrt{7}}=\frac{a^3\sqrt{105}}{42}$.