Chọn C

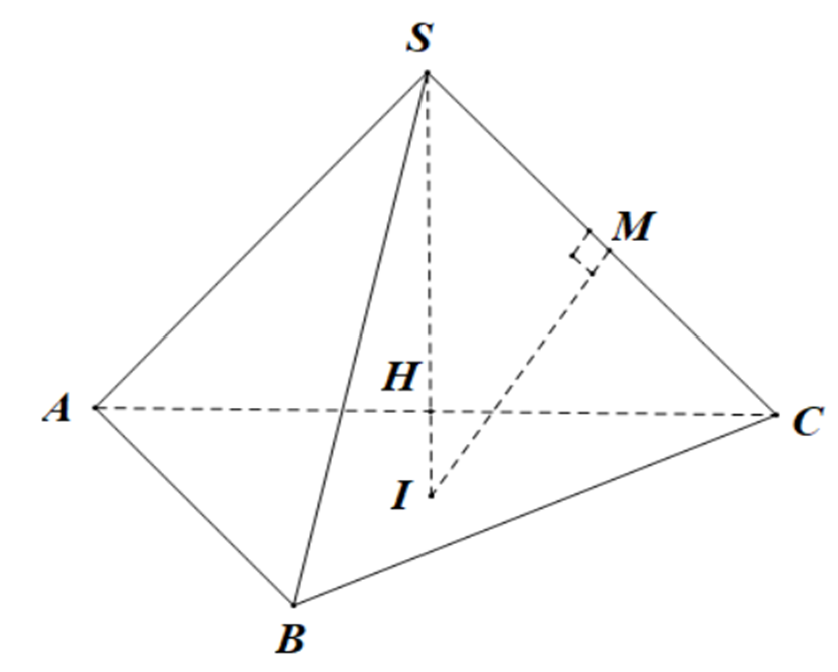
Ta có SB = SC = 2, $\widehat{BSC}=60°$ suy ra tam giác BSC đều => BC =2.

Lại có SA = SC = 2, $\widehat{ASB}=90°$ suy ra tam giác ASB vuông cân tại S $\Rightarrow AB=2\sqrt{2}$.

Mặt khác, SA = SC = 2, $\widehat{ASB}=120°$, áp dụng định lí cosin cho tam giác ASC, ta được:

$A{C}^2=S{A}^2+S{C}^2-2SA.SC.cos\widehat{ASC}={3.2}^2\iff AC=2\sqrt{3}$.

Xét tam giác ABC có $B{C}^2+A{B}^2=2^2+{\left(2\sqrt{2}\right)}^2=12=A{C}^2$ suy ra tam giác ABC vuông tại B.

Gọi H là trung điểm của cạnh AC suy ra H là tâm đường tròn ngoại tiếp tam giác ABC.

Mà SA = SB = SC $\Rightarrow SH\perp \left(ABC\right)$.

Trong mặt phẳng (SAC) kẻ đường trung trực canh SC cắt đường thẳng SH tại I suy ra là tâm mặt cầu ngoại tiếp hình chóp.

Xét tam giác vuông ASH vuông tại H có $SH=\sqrt{S{A}^2-A{H}^2}=\sqrt{2^2-{\left(\frac{2\sqrt{3}}{2}\right)}^2}=1$.

Ta có $\Delta SHC~\Delta SMI\Rightarrow \frac{SI}{SC}=\frac{SM}{SH}\iff SI=\frac{SM.SC}{SH}=2$

Diện tích mặt cầu ngoại tiếp chóp là. $S=4\pi R^2=16\pi$.