Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi M, N, P lần lượt là trọng tâm của ba tam giác SAB, SBC, SCA

Bài 20 trang 95 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có SA ⊥ (ABC). Gọi M, N, P lần lượt là trọng tâm của ba tam giác SAB, SBC, SCA. Chứng minh rằng SA ⊥ (MNP).

Trả lời

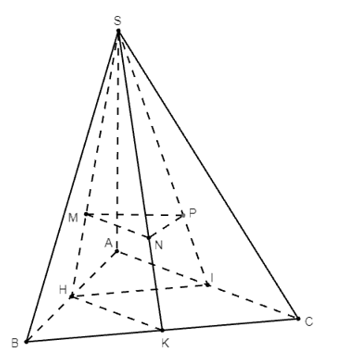
Gọi H, K, I lần lượt là trung điểm của AB, BC, CA.

Vì M, N, P lần lượt là trọng tâm của ba tam giác SAB, SBC, SCA nên ta có:

$\frac{SM}{SH}=\frac{SN}{SK}=\frac{SP}{SI}=\frac{2}{3}$.

Theo định lý Thalès: MN // HK, MP // HI.

Mà HK ⊂ (ABC), IH ⊂ (ABC).

Suy ra: MN // (ABC), MP // (ABC).

Trong (MNP) có: MN ∩ MP = M, MN // (ABC), MP // (ABC).

Suy ra (MNP) // (ABC).

Lại có SA ⊥ (ABC) nên SA ⊥ (MNP).

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác: