Giải SBT Toán 11 (Cánh diều) Bài 1: Hai đường thẳng vuông góc

Giải SBT Toán 11 Bài 1: Hai đường thẳng vuông góc

Bài 1 trang 88 SBT Toán 11 Tập 2: Cho hình lăng trụ ABC.A’B’C’ có ABC là tam giác đều và ABB’A’ là hình chữ nhật. Gọi M là trung điểm của BC (Hình 4).

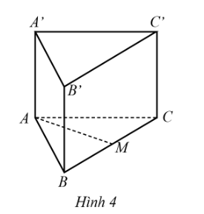
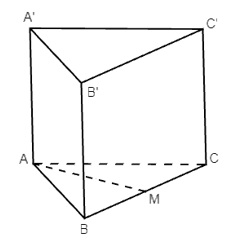
a) Số đo giữa hai đường thẳng AB và B’C’ bằng:

A. 30°;

B. 45°;

C. 60°;

D. 90°.

b) Số đo giữa hai đường thẳng AB và CC’ bằng:

A. 30°;

B. 45°;

C. 60°;

D. 90°.

c) Số đo giữa hai đường thẳng AM và A’C’ bằng:

A. 30°;

B. 45°;

C. 60°;

D. 90°.

Lời giải:

a) Đáp án đúng là: C

Do tam giác ABC đều nên $\widehat{ABC}=60°$.

Ta có: BC // B’C’ nên $\left(AB,B^{\text{'}}{C}^{\text{'}}\right)=\left(AB,BC\right)=\widehat{ABC}=60°$.

b) Đáp án đúng là: D

Do ABB’A là hình chữ nhật nên $\widehat{AB{B}^{\text{'}}}=90°$.

Ta có: BB’ // CC’ nên $\left(AB,C{C}^{\text{'}}\right)=\left(AB,B{B}^{\text{'}}\right)=\widehat{AB{B}^{\text{'}}}=90°$.

c) Đáp án đúng là: A

Do tam giác ABC đều, AM là đường trung tuyến nên AM cũng là đường phân giác của $\widehat{BAC}$.

Suy ra: $\widehat{MAC}=\frac{1}{2}\widehat{BCA}=30°$.

Ta có: AC // A’C’ nên $\left(AM,A^{\text{'}}{C}^{\text{'}}\right)=\left(AM,AC\right)=\widehat{MAC}=30°$.

Bài 2 trang 89 SBT Toán 11 Tập 2: Hình 5 gợi nên hình ảnh một số cặp đường thẳng vuông góc với nhau. Hãy chỉ ra ba cặp đường thẳng vuông góc với nhau.

Lời giải:

Ba cặp đường thẳng vuông góc với nhau có thể là: a và b, b và c, c và d.

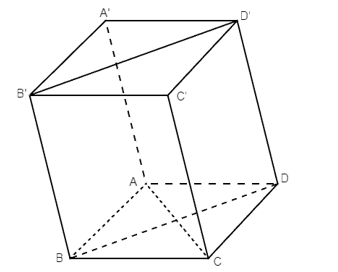
Bài 3 trang 89 SBT Toán 11 Tập 2: Cho hình hộp ABCD.A’B’C’D’ có đáy là hình vuông.

a) Chứng minh rằng AB ⊥ A’D’ và AC ⊥ B’D’.

b) Tính góc giữa hai đường thẳng AC và A’B’.

Lời giải:

a) ⦁ Do ABCD.A’B’C’D’ là hình hộp nên A’D’ // AD (tính chất hình hộp).

Mà AB ⊥ AD (vì ABCD là hình vuông)

Từ đó, suy ra AB ⊥ A’D’.

⦁ Do ABCD.A’B’C’D’ là hình hộp nên ta có BB’ // DD’ và BB’ = DD’.

Suy ra B’D’DB là hình bình hành nên ta có B’D’ // BD.

Mà AC ⊥ BD (vì ABCD là hình vuông)

Từ đó, suy ra AC ⊥ B’D’.

b) Xét hình vuông ABCD có: $\widehat{CAB}=\frac{1}{2}\widehat{DAB}=45°$.

Mà AB // A’B’ nên $\left(AC,A^{\text{'}}{B}^{\text{'}}\right)=\left(AC,AB\right)=\widehat{CAB}=45°$.

Vậy góc giữa hai đường thẳng AC và A’B’ bằng 45°.

Bài 4 trang 89 SBT Toán 11 Tập 2: Cho hình lăng trụ MNPQ.M’N’P’Q’ có tất cả các cạnh bằng nhau. Chứng minh rằng M’N ⊥ P’Q.

Lời giải:

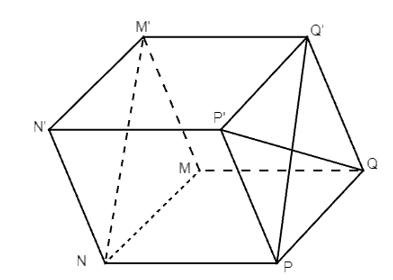
Do MNPQ.M’N’P’Q’ là hình lăng trụ có tất cả các cạnh bằng nhau nên PQ = QQ’ = P’Q’ = PP’. Suy ra PQQ’P’ là hình thoi nên có: P’Q ⊥ PQ’. (1)

Tương tự: ta cũng có M’Q’QM và MQPN là hai hình thoi.

Suy ra:

⦁ NP // MQ mà MQ // M’Q’ nên NP // M’Q’.

⦁ NP = MQ mà MQ = M’Q’ nên NP = M’Q’.

Từ đó, ta có: NPQ’M’ là hình bình hành, suy ra M’N // PQ’. (2)

Từ (1), (2) ta có: M’N ⊥ P’Q.

Bài 5 trang 89 SBT Toán 11 Tập 2: Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của AB và CD. Tính góc giữa hai đường thẳng AD và BC, biết $MN=a\sqrt{3}$và AD = BC = 2a.

Lời giải:

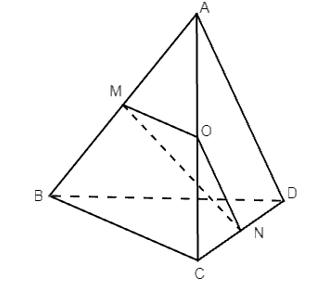
Gọi O là trung điểm AC.

Do O, M lần lượt là trung điểm AC và AB nên OM là đường trung bình của tam giác ABC.

$\Rightarrow OM=\frac{1}{2}BC=a$ và OM // BC.

Tương tự ta có: ON là đường trung bình của tam giác ACD.

$\Rightarrow ON=\frac{1}{2}AD=a$ và ON // AD.

Khi đó: (AD, BC) = (ON, OM).

Xét tam giác MON, theo hệ quả định lí Cosin ta có:

$\cos \widehat{MON}=\frac{O{M}^2+O{N}^2-M{N}^2}{2OM.ON}=\frac{a^2+a^2-{\left(a\sqrt{3}\right)}^2}{2a.a}=-\frac{1}{2}$.

Nên $\widehat{MON}=120°$.

Suy ra: $\left(AD,BC\right)=\left(ON,OM\right)=180°-\widehat{MON}=180°-120°=60°$.

Vậy góc giữa hai đường thẳng AD và BC là 60°.

Xem thêm các bài giải SBT Toán lớp 11 Cánh diều hay, chi tiết khác: