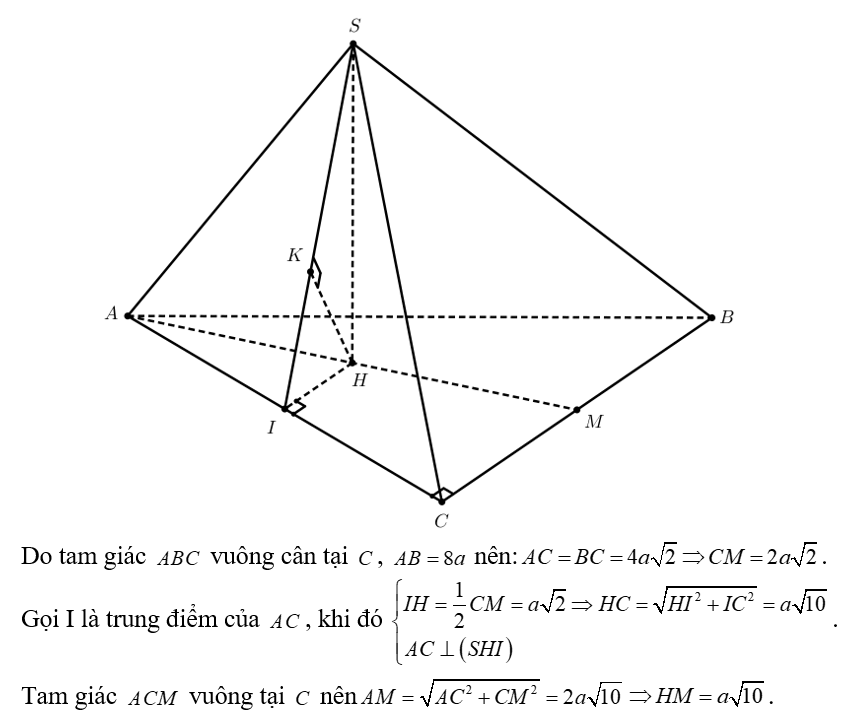
Cho hình chóp SABC có đáy là tam giác vuông cân tại C , cạnh huyền có độ dài bằng 8a . Gọi M là trung điểm của BC
Cho hình chóp SABC có đáy là tam giác vuông cân tại C , cạnh huyền có độ dài bằng 8a . Gọi M là trung điểm của BC , hình chiếu vuông góc của S xuống mặt phẳng (ABC) là trung điểm H của AM và . Khoảng cách từ đến mặt phẳng (ABC) là:
A.
B.
C.
D.