Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA  (ABC), SA= a căn 2 . Khoảng cách từ A đến mặt phẳng (SBC) bằng

Trả lời

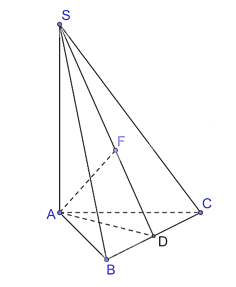
Kẻ AD ^ BC tại D.

Vì SA ^ (ABC) nên SA ^ BC mà AD ^ BC nên BC ^ (SAD), suy ra (SBC) ^ (SAD).

Kẻ AF ^ SD tại F.

Vì (SBC) ^ (SAD), (SBC) Ç (SAD) = SD, AF ^ SD nên AF ^ (SBC).

Suy ra d(A, (SBC)) = AF.

Vì tam giác ABC đều cạnh a, AD là đường cao nên AD = $\frac{a\sqrt{3}}{2}$ .

Vì SA ^ (ABC) nên SA ^ AD hay tam giác SAD vuông tại A.

Xét tam giác SAD vuông tại A, AF là đường cao nên ta có

 $\frac{1}{A{F}^2}=\frac{1}{S{A}^2}+\frac{1}{A{D}^2}=\frac{1}{2a^2}+\frac{4}{3a^2}=\frac{1}{2a^2}+\frac{4}{3a^2}=\frac{11}{6a^2}\Rightarrow AF=\frac{\sqrt{66}a}{11}$ .

Vậy d(A, (SBC)) = $\frac{\sqrt{66}a}{11}$  .