Cho hình chóp S. ABCD có đáy ABCD là nửa lục giác đều nội tiếp đường tròn đường kính

Trả lời

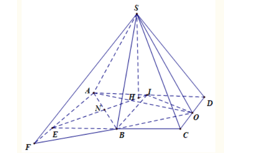
Gọi I, N là trung điểm của AD, AB. Gọi H là tâm đường tròn ngoại tiếp tam giác ABO, vì tam giác ABI đều nên H thuộc NI.

Kẻ HK vuông góc CD, dựng hình bình hành AECD. Gọi F là giao điểm của BO và AE.

Ta có: $AF\text{// }CD,$ nên $d(SA,CD)=d(CD,(SAF\left)\right)=d(O,(SAF\left)\right).$

Vì ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AD, nên tam giác BIC và CID là các tam giác đều, do đó ta có:

$\begin{array}{l}AC=\sqrt{{\left(4a\right)}^2-{\left(2a\right)}^2}=2a\sqrt{3}\\ CO=\frac{1}{2}CD=a\\ AO=\sqrt{A{C}^2+C{O}^2}=\sqrt{12a^2+a^2}=a\sqrt{13}\\ BO=\sqrt{B{C}^2+C{O}^2-2BC.CO.{\text{cos120}}^0}=\sqrt{4a^2+a^2+2a^2}=a\sqrt{7}\\ S_{\Delta ABO}=\frac{(2a+4a).a\sqrt{3}}{2}-\frac{1}{2}.2a.\frac{a\sqrt{3}}{2}-\frac{1}{2}.4a.\frac{a\sqrt{3}}{2}=\frac{3a^2\sqrt{3}}{2}.\end{array}$

Suy ra

 $\begin{array}{l}AH=\frac{2a.a\sqrt{7}.a\sqrt{13}}{4.\frac{3a\sqrt{3}}{2}}=\frac{a\sqrt{273}}{9}.\\ SH=\sqrt{S{A}^2-A{H}^2}=\sqrt{4a^2-\frac{273a^2}{81}}=\frac{a\sqrt{51}}{9}.\end{array}$

Diện tích $S_{\Delta AFO}=2S_{\Delta ABO}=3a^2\sqrt{3}.$

Thể tích của khối chóp S. AFO là: $V_{S.AFO}=\frac{1}{3}SH.S_{AFO}=\frac{a^3\sqrt{153}}{9}.$

Diện tích tam giác SAF:

$SA=2a,AF=3a\Rightarrow S{B}^2=\frac{S{O}^2+S{F}^2}{2}-\frac{F{O}^2}{4}\Rightarrow SF=3a\sqrt{2}\Rightarrow S_{\Delta SAF}=\frac{a^2\sqrt{119}}{4}.$

Vậy $d(SA,CD)=d(CD,(SAF\left)\right)=d(O,(SAF\left)\right)=\frac{3V_{O.SAF}}{S_{\Delta SAF}}=\frac{3\frac{a^3\sqrt{153}}{9}}{\frac{a^2\sqrt{119}}{4}}=\frac{2a}{\sqrt{7}}.$