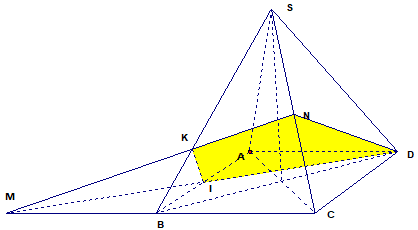
Cho hình chóp đều SABCD có tất cả các cạnh bằng a. Gọi M là điểm đối xứng của C qua B và N là trung điểm SC , mp( DMN) chia khối chóp SABCD thành
Cho hình chóp đều SABCD có tất cả các cạnh bằng a. Gọi M là điểm đối xứng của C qua B và N là trung điểm SC , chia khối chóp SABCD thành hai phần . Tính tỉ số thể tích của hai phần đó.