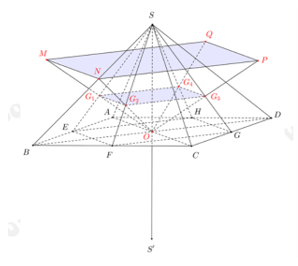
Cho hình chóp đều S. ABCD có cạnh đáy bằng a, cạnh bên bằng 2a và O là tâm của đáy. Gọi M, N, P và Q lần lượt là các điểm đối xứng với O qua trọng tâm của các tam giác SAB, SBC, SCD, SDA và là điểm đối xứng của S qua O. Tính thể tích của khối chóp S.MNPQ

Gọi $G_1,G_2,G_3,G_4$ lần lượt là trọng tâm của các tam giác SAB, SBC, SCD, SDA.

Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

Ta có: $S_{MNPQ}=4S_{G_1{G}_2{G}_3{G}_4}=4.\frac{4}{9}.S_{EFGH}=4.\frac{4}{9}.\frac{1}{2}.EG.HF=\frac{8a^2}{9}.$

Mặt khác:

$\begin{array}{l}d(S^{\text{'}},(MNPQ\left)\right)=d(S^{\text{'}},(ABCD\left)\right)+d(O,(MNPQ\left)\right)\\ =d(S,(ABCD\left)\right)+2d(O,(G_1{G}_2{G}_3{G}_4\left)\right)\\ =d(S,(ABCD\left)\right)+\frac{2}{3}d(S,(ABCD\left)\right)\\ =\frac{5}{3}d(S,(ABCD\left)\right)=\frac{5a\sqrt{14}}{6}.\end{array}$

Vậy thể tích của khối chóp S.MNPQ là:

$V_{S^{\text{'}}.MNPQ}=\frac{1}{3}.\frac{5a\sqrt{14}}{6}.\frac{8a^2}{9}=\frac{20a^3\sqrt{14}}{81}.$