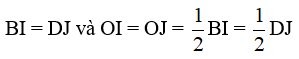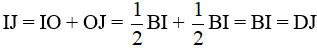Cho hình bình hành ABCD tâm O. Gọi M,  theo thứ tự là trung điểm của BC, AD. Gọi I, J lần lượt

Bài 4.59 trang 70 SBT Toán 10 Tập 1: Cho hình bình hành ABCD tâm O. Gọi M,  theo thứ tự là trung điểm của BC, AD. Gọi I, J lần lượt là giao điểm của BD với AM, CN. Xét các vectơ khác  có đầu mút lấy từ các điểm A, B, C, D, M, N, I, J, O.

a) Hãy chỉ ra những vectơ bằng vectơ $\overrightarrow{AB};$ những vectơ cùng hướng với $\overrightarrow{AB};$ 

b) Chứng minh rằng BI = IJ = JD.

Trả lời

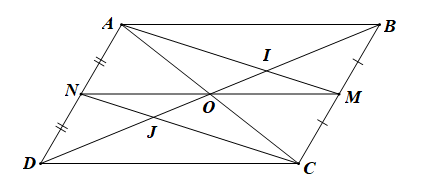
a) ABCD là hình bình hành có M, N lần lượt là trung điểm của BC, AD

Nên MN là đường trung bình của hình bình hành

$\Rightarrow$ MN // AB // DC và MN = AB = DC.

$\Rightarrow$ $\overrightarrow{AB}=\overrightarrow{DC}=\overrightarrow{MN}$

Vậy những vectơ bằng vectơ $\overrightarrow{AB}$ là: $\overrightarrow{AB};\overrightarrow{DC};\overrightarrow{MN}.$

Lại có O là tâm hình bình hành nên O là trung điểm của AC và BD

Do đó NO là đường trung bình của DADC

$\Rightarrow$ NO // DC

Chứng minh tương tự ta cũng có OM // DC

Do đó ba điểm M, O, N thẳng hàng.

Vậy những vectơ cùng hướng với $\overrightarrow{AB}$ là: $\overrightarrow{AB},\overrightarrow{NO},\overrightarrow{OM},\overrightarrow{NM},\overrightarrow{DC.}$

b) Xét tam giác ABC có: AM, BO là hai đường trung tuyến của tam giác

Mà AM cắt BO tại I

Do đó I là trọng tâm của DABC.

$\Rightarrow BI=\frac{2}{3}BO$ và $OI=\frac{1}{2}BI$ (tính chất trọng tâm)   (1)

Tương tự ta cũng có J là trọng tâm của DADC.

$\Rightarrow DJ=\frac{2}{3}DO$ và $OJ=\frac{1}{2}DJ$ (tính chất trọng tâm)  (2)

Mặt khác BO = DO (do O là trung điểm của BD)   (3)

Từ (1), (2) và (3) ta có: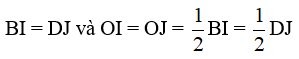 

Mà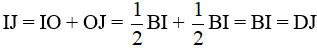 

Vậy BI = IJ = JD.

Xem thêm các bài giải SBT Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vectơ

Bài tập cuối chương 4

Bài 12: Số gần đúng và sai số

Bài 13: Các số đặc trưng đo xu thế trung tâm

Bài 14: Các số đặc trưng đo độ phân tán